Assignment 6

Explorations of the Medial Triangle using Geometer's Sketchpad

by Rives Poe

Fact: For any equilateral triangle, the triangle of the medians will always be an equilateral triangle.

Reason: Because a medial triangle is constructed from the midpoints of an original triangle and an equilateral triangle has 3 congruent sides, the sides of the medial triangle will all be congruent as well.

 

Equilateral Triangle ABC and it's Medial Triangle IJK

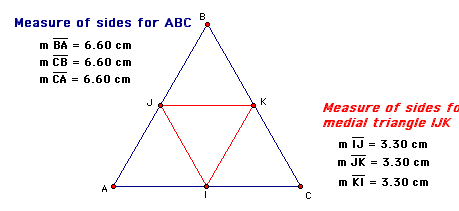
Now, let's see if this holds true for isosceles triangles. What do you think? All sides are not equal in an isosceles triangle, but will the midpoints generate an isosceles triangle of medians? Take a look below, then try some sketches of your own.

 

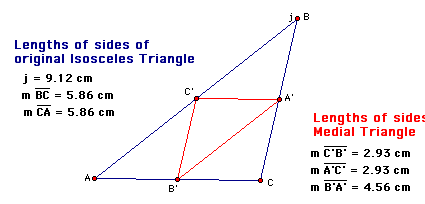
Obtuse Isosceles Triangle ABC and it's Medial Triangle A'B'C'

In the example qbove, the original isosceles triangle generates an isosceles triangle of medians. Let's take a look at a different isosceles triangle.

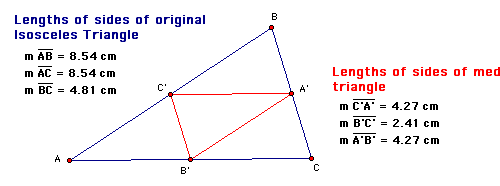
Acute Isosceles Triangle ABC and it's Medial Triangle A'B'C'

Why does the original triangle generate the same type of medial triangle is a question you might be asking yourself right now. Here we go with an explanation, so pay attention!

A triangle of medians originates from the midpoints of an original triangle. In the constructions above you will notice that segment A'B', is parallel to AB and it is exactly half the length. Same thing goes for side C'B', it too is parallel to side CB and it is exactly half of the length. Pretty simple, right?

 

Let's try something else, since we are on a roll! Say we have a right triangle, do you think it's median triangle will also be a right triangle or do you think this will only occur under certain circumstances? Take a look below.

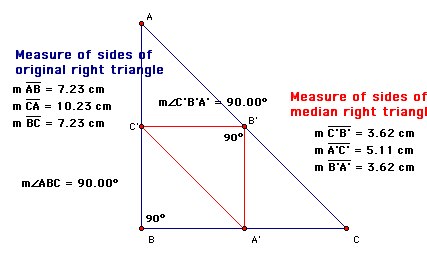
Right Triangle ABC and it's median triangle A'B'C'

In the example above, the original isosceles RIGHT triangle generates an isosceles RIGHT triangle of medians. This will be the case for all right triangles.

As we discovered earlier, the medial triangle is always similar to the original triangle. The lengths of the sides of the medial triangle are always half the length of the original. Therefore all the angles are congruent. Look at the figure above. Angle B' is opposite and congruent to angle B. The same thing goes for angle C and C' and angle A and A'.

 

I hope you feel smarter and have a better understanding of THE TRIANGLE OF MEDIANS!!!!


 

RETURN to home page