Assignment 7

Tangent Circles

by Rives Poe

For the following two circles, I am going to construct a circle tangent to them both.

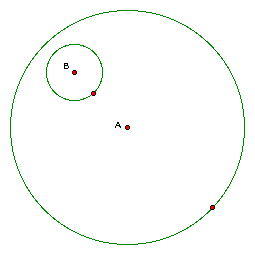As you can see, the smaller circle, with center B is inside the larger circle, with center A. Using GSP allows me to construct a the tangent circle quicker than by hand.

 

I will first pick any point on the large circle and construct a line through that point and the center of the large circle:

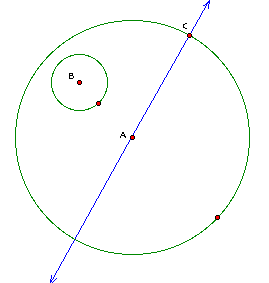Next I will construct a segment from the center of the small circle, point B, to point C, which I selected earlier:

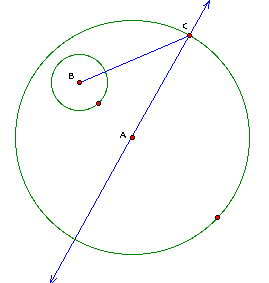From here, I will construct a circle using the radius of the small circle (circle with center B) and point C on the large circle:

 

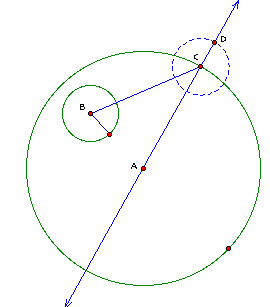Next, I will construct a segment from the center of the small circle to the intersection of the new small circle, with center C, and the line that extends through pointA and pointC and find it's midpoint. From the midpoint, I will construct a line perpendicular to the segment I will have just created.

 

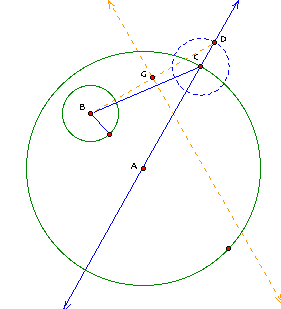Now, mark the intersection where the perpendicular line crosses segment AC. I will use this intersection as the center of my circle that is tangent to the two circles. The radius will be from this new intersection to point C.

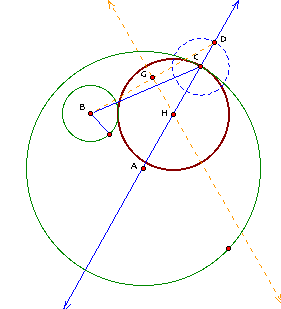The maroon circle is tangent to my first two circles.

To see an animation of the tangent circle, click here.

To use a script tool to create your own circle tangent to two circles, click here.

Be sure to move the circles around and notice that no matter where they are, the maroon circle is always tangent to both of them.

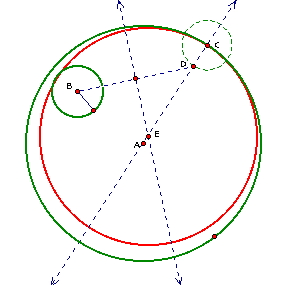
Well, we are not finished yet with tangent circles! There is another circle that is tangent to my original green circles. Below I have constructed the second tangent circle (it is red!). It is constructed in a similar way to the first tangent circles, except I constructed a segment from my original small circle to the lower intersection of the circle with center C. I used segment EC as the radius for the tangent circle.

Click here to see an animation of the tangent circle.

Now I think we should look at what happens when we trace the centers of the tangent circles.

Click here to see an animation of the first tangent circle.

Click here to see an animation of the second tangent circle I constructed.

 

This is what should have happened when you clicked the "animate point" button on the GSP file.

 

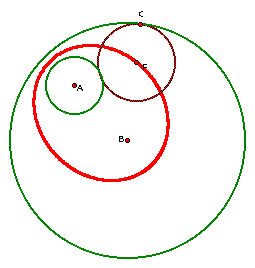Hopefully this is what happened when you clicked the "animate point" button on GSP. What is happening?

To finish this investigation we can say that it is apparent that the center of the tangent circle ( the loci) forms an ellipse.

 

 

 

RETURN to home page