

In this exploration, we are going to observe how the Pedal Triangle changes depending upon the pedal point's location. Sit back and get ready to observe!
First of all, I constructed triangle ABC. From triangle ABC, I put an arbitrary point on the page and constructed perpendicular lines to the sides of ABC. The three points where the perpendiculars cross the triangle is the pedal triangle RST. Here is the construction below:

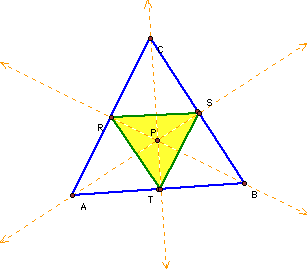
If pedal point P is the centroid of triangle A, the pedal triangle will look like this:
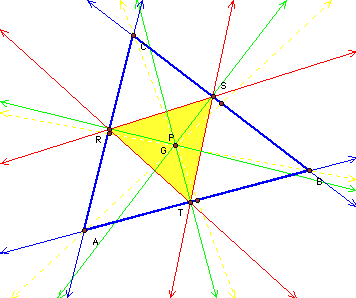
If the pedal point P is the Incenter:
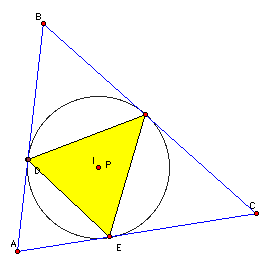
If pedal point P is the Orthocenter:
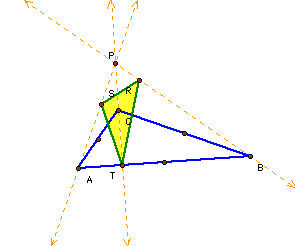
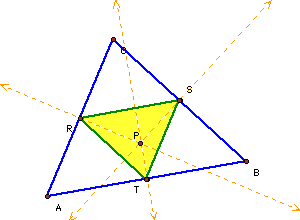
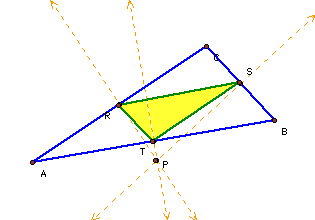
Let's see what happens when the pedal point falls on the center of the nine point circle.
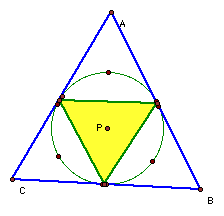
What if P is on a side of the triangle?
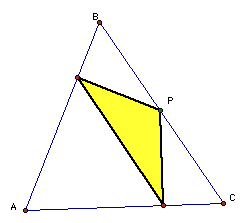
What if P is on a vertex of triangle ABC?
Return to home page