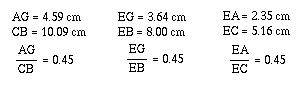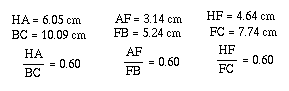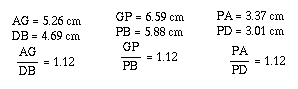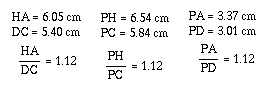Final Assignment

by Rives Poe

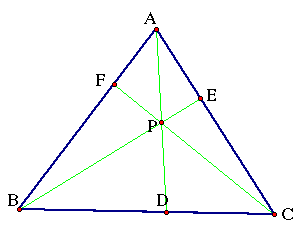
For this assignment, we will start by constructing a triangle ABC. Then select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D,E, and F respectively. Below is such aconstruction.

Now, let's explore (AF)(BF)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

Click here to see and manipulate a GSP sketch for different locations of P.

 

In this sketch you should have noticed that (AF)*(BF)*(EC) = (FB)*(DC)*(EA).

So, we see that they are equal, but we need to prove it!

Here goes nothing!

First we need to construct parallel lines to produce similar triangles.

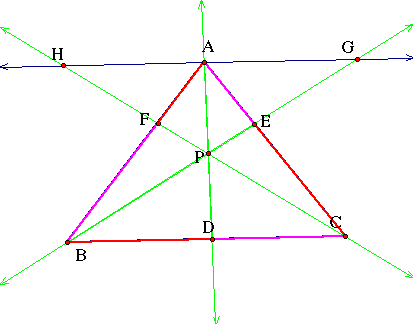(Line HG is parallel to segment BC. )

First we can see that triangles EGA and ECB are similar:

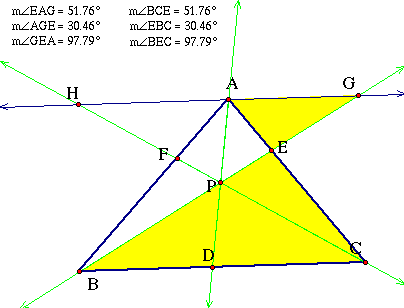
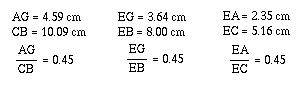Therefore: AG/BC = GE/EB = AE/CE.

 

Triangle FAH is similar to triangle FBC.

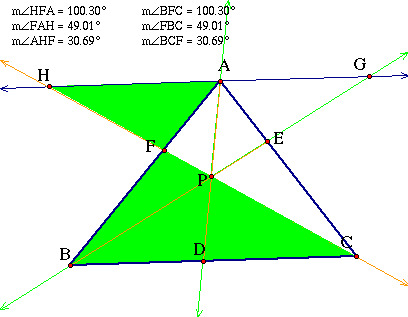
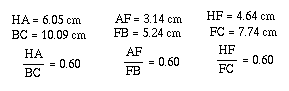Therefore, HA/BC = FA/FB = FH/FC

 

Triangles AGP and DBP are similar:

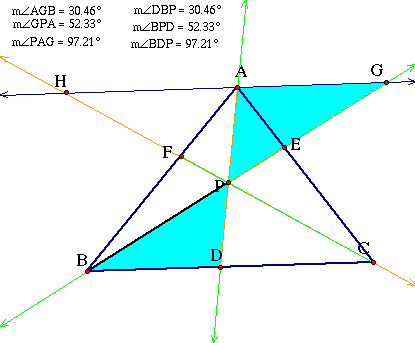
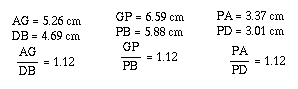Thus, AG/DB = GP/PB = AP/PD

 

And finally, triangle HAP is similar to triangle CDP:

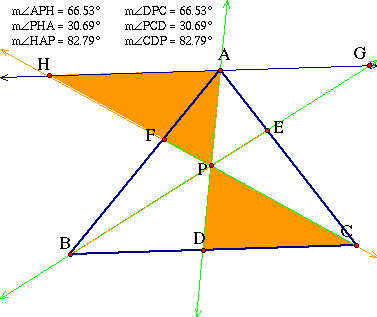
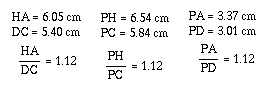Therefore, AH/DC = AP/DP = HP/PC.

Now we need to pull all of this information together to see if we can prove:

(AF)(BD)CE)/(BF)(CD)(AE) = 1.

So, we need to gather some information from above. We don't need all of the ratios, just a few that are going to help us find the above ratio.

1. AG/BC =AE/CE

2.BC/HA = FB/FA

3. AH/DC= AG/DB**

**we can find use this ratio because the ratios of triangle AGP and DBP are similar to the ratios of triangles AHP and DCP.

So, when we multiply the above ratios together we get:

(AG/BC)(BC/HA)(AH/DC) = (AE/CE)(FB/FA)(AG/DB)

some things cancel out, so we are left with:

AG/DC = (AE/CE)(FB/FA)(AG/DB)

let's multiply the left side by DB/AG, so that we now have on the left DB/DC.

Now, if we move everything to the left we have:

(DB/DC)(CE/EA)(FA/FB) = 1

And there is our proof that the ratio of the sides equals 1!!!

Click here to see a GSP sketch of the triangle with lines, so that we can move P outside of the triangle.

Click here to see a construction showing that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. The ratio is equal to 4 when P falls on the centroid of ABC.

 

 

 

Return to Rives' home page