Assignment 4: Centers of a Triangle
Writeup:
Triangle properties were explored, but I'll take advantage of this write-up opportunity to show off my cool engine.
To run this engine click here: GSP File: To see the equation for height as a
function of rotation angle click: Graphing Calc
File
I believe that by taking a bit of extra time to put these geometric constructions into real-life examples we can generate greater interest in our students and gain better long term retention. The more the students relate math to their everyday experiences, the more they will recall their math lessons when they see these principles in action. The more they relate math to solving real world problems, the more they will apply mathematical thinking and logic in many domains of their everyday existence (much needed).
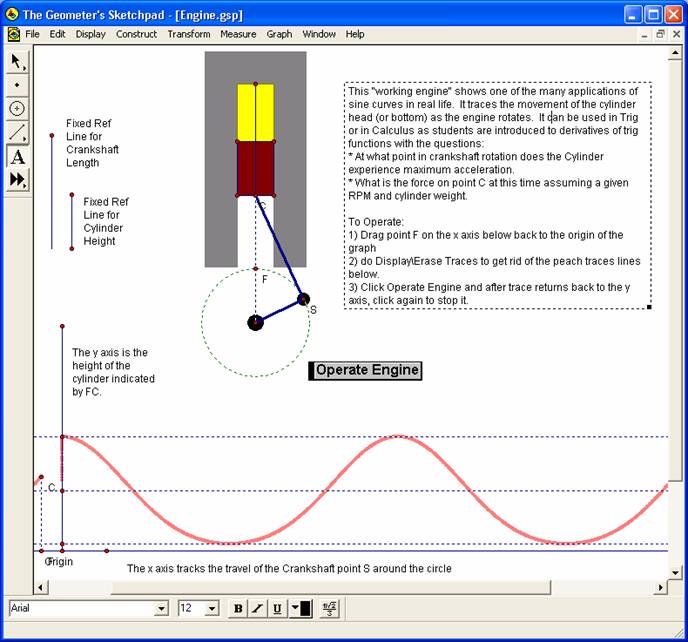
The unexpected properties of the curve
At first I expected (just blindly assumed) a sine curve. GSP uncovered interesting characteristics though - as is apparent in looking at the curve above which clearly has a longer period on the bottom than it does on top. The curve appears to be the combination of a sine curve and a cycloid. This makes some sense because it is the combination of pure vertical movement, which is a sine curve, with the influence of the movement in the x axis through the connecting rod.
So, the challenge is to find out the exact formula for the curve above. Should be relatively straightforward given the basic geometry\trigonometry of the mechanism (sine, cosine, Pythagorean, etc.). I marked up an enlarged copy of the above crank to explore.
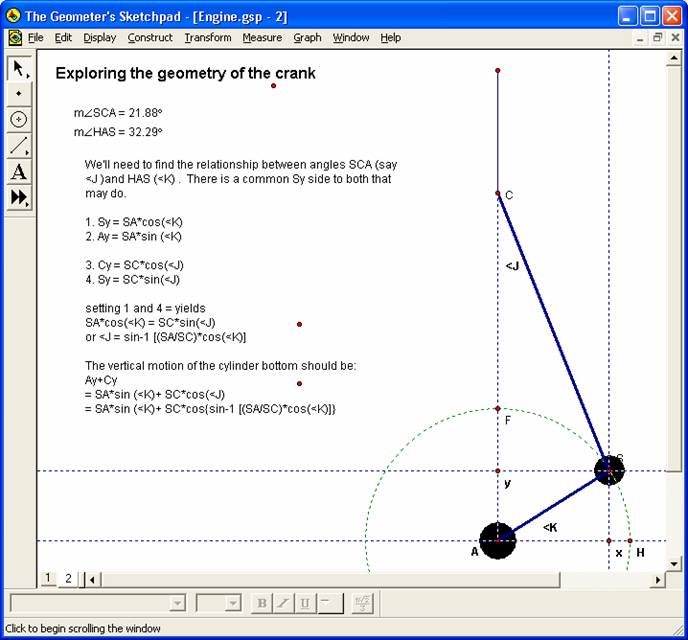
The basic geometry yields the formula Height = SA*sin (<K)+ SC*cos{sin-1 [(SA/SC)*cos(<K)]}
There must be a good way to simplify this equation but I can't find it in reasonable order. I re-found that arcsin(cos(x)) = pi/2 – x, but it is unclear what the impact of SA/SC is on the ability to simplify this equation – my trig is a bit too rusty at this level.
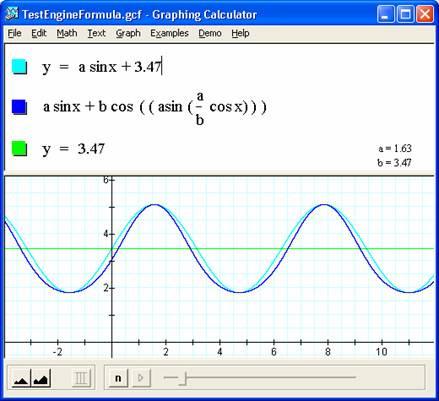
Fortunately, Graphing calculator is forgiving and accepts this equation as is. The plot below, using the actual measures of the crank and connecting rod in our engine, maps well to the real deal so all appears well.
Notes on Other Problems
This Assignment has a set of activities to help become familiar with GSP and to review some basic geometry. After examining the activitites in the assignment, pick some topic for a brief write-up. The write-up could be one of the proofs, but does not have to be. It could be some exploration you would try with students. Or you might take one of the topics (e.g. medians) and explore some of the standard geometry for the topic.
To see the following in GSP click on these links
1. The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.
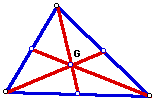
The centroid is the center of gravity and always remains within the bounds of triangle.
As center of gravity it is "weighted" toward the fat side of the median by ratio of 1/3 to 2/3.
2. The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes.
Use GSP to construct an orthocenter H and explore its location for various shapes of triangles. (Make sure your construction holds for obtuse triangles.)
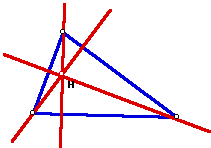
Orthocenter is all over the place. Hard to visualize constructs for obtuse angles but holds true. Always sits on the vertex of a right triangle. As triangle squishes with obtuse near 180, the orthocenter goes out to infinity.
3. The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
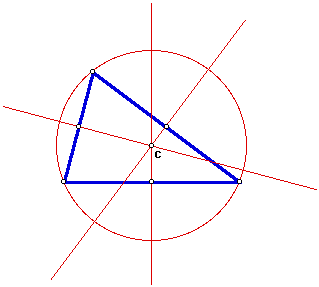
Circumcenter lies on the hypotenuse of a right triangle. Like Orthocenter, as triangle squishes with obtuse near 180, the orthocenter goes out to infinity.
4. The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
Use GSP to find a construction of the incenter I and explore its location for various shapes of triangles. The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle.
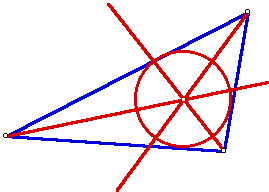
Behavior very similar to centroid. Always inside the triangle and very stable. As an obtuse angle reached 180, the incenter meets the vertex of obtuse angle.
5. Use GSP to construct G, H, C, and I for the same triangle. What relationships can you find among G, H, C, and I or subsets of them? Explore for many shapes of triangles.
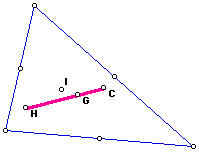
Orthocenter (H) and Circumcenter (C ) seem related and the Centroid (G) and Incenter (I) appear similar.
Centroid is most apparently the 'center' of the circle around which the other points fly. All converge for equilateral triangle.
H and C move about by far most actively on opposite sides of G and three always form a line. Both move to ∞ as obtuse moves to 180. For a right triangle, H is always at vertex and C at midpoint of hypotenuse. H is always 2x as far from G as C.
I and G move to vertex of obtuse as it approaches 180.
Try to get H to go through midpoint of a side but very unstable. Investigate
6. Take any triangle. Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. Construct G, H, C, and I for this new triangle. Compare to G, H, C, and I in the original triangle.

If m indicates medial triangle and b represents big triangle, then:
Gm and Gb always same point
Hm and Cb always same point
G C and H for both m and b always lie on the same lie
Ib and Im always on opposite sides of this line, if not both on it. Ib always 2x as far from G as Im.
7. Take any acute triangle. Construct a triangle connecting the feet of the altitudes. This is called the ORTHIC triangle. Construct G, H, C, and I for the orthic triangle. Compare to G, H, C, and I in the original triangle. Can you extend this to right triangles or obtuse triangles?
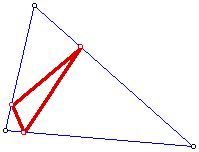
Let O indicate Ortic triangle and b indicate big circumscribing triangle, then:
Io and Hb always same point
Co always lies on the line formed by HGand C of b.
Note there is no orthic triangle in GSP if b is obtuse triangle, though probably an artifact of the termination of triangle legs at vertex. If we allowed feet of orthic triangle to traverse out beyond bounds of triangle then it would inverse.
8. Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.
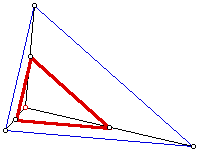
9. In the same original triangle, construct the three secondary triangles of Exercises 6, 7, and 8. Construct the circumcircle for each of the secondary triangles. What do you observe? Can you prove your conjecture?
10. The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. Construct the nine points, locate the center (N) and construct the nine point circle.
11. How is N related to G, H, C, or I for different shaped triangles?
12. Prove that the three perpendicular bisectors of the sides of a triangle are concurrent.
13. Prove that the lines of the three altitudes of a triangle are concurrent.
14. Prove that the three medians of a triangle are concurrent and that the point of concurrence, the centroid, is two-thirds the distance from each vertex to the opposite side.
How would you use GSP to help students understand this relationship of the triangle and its medians? How would you develop a sense of proof of the relationship with students?
15. Prove that the three angle bisectors of the internal angles of a triangle are concurrent.
16. Prove that any angle bisector of a triangle is concurrent with the two angle bisectors of the opposite exterior angles of a triangle.
17. Take a point of concurrence as determined in Problem 16 and construct a circle tangent to the lines of the three sides (of the triangle)
18. Prove that for any triangle, H, G, and C are collinear, and prove that HG = 2GC.