Assignment Final
Click the GSP File to run these problems.
A. Consider any triangle ABC.
Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
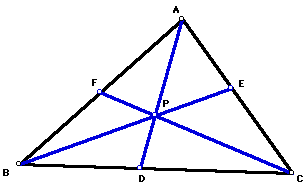
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
Exploration
As hinted, the product of the three lengths is always equal, so conjecture this must be true.
Tried to find other relationships, but there are so many
other potential ratios it is difficult, so proceed along the suggested relationship
B.
Conjecture? Prove it!
(you may need draw some parallel lines to produce some similar triangles) Also, it probably helps to consider the ratio
![]()
Sketch 1
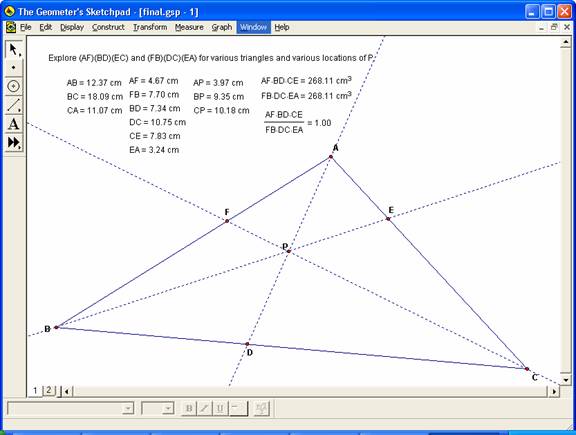
Utilizing the hints to locate complementary angles, we draw the sketch below and find a wealth of similar triangles
The angles above are marked in color coded pairs to better see the equivalents. The angle equalities are generally found by alternate interior angles or vertical angles. From above = angles, we have three sets of similar triangles by virtue of three equal angles:
* Blue – with angles An, As, and Ao
* Green – with angles Ap, At, and Al.
*
Blue + Green – with angles
Since we're trying to justify the ratio of sides, lets start putting these similarities into that form. Similar triangles have a constant ratio for the corresponding sides, so:
Blue – with angles An, As, and Ao
AP/DP = JP/CP = JA/CD
Green – with angles Ap,
At, and Al.
AP/DP = KP/BP = KA/BD
Blue + Green – with angles
(may not give anything new)
We can see that both blue and green equalities are equal by virtue of AP/DO ratio in both, so combine these two to form:
AP/DP = JP/CP = JA/CD = KP/BP = KA/BD
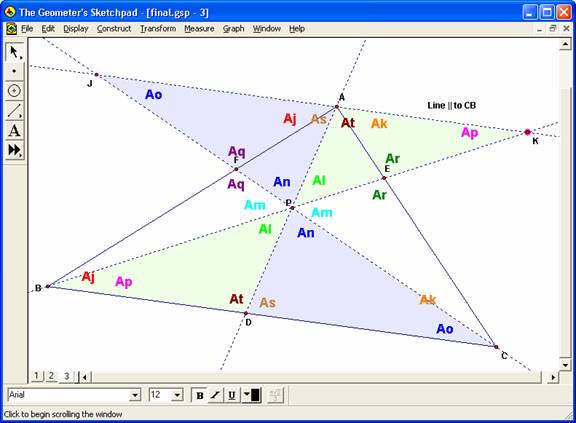
Sketch 2
We also have the equivalent triangles below:

Using the same techniques we have similar triangles:
* Blue – with angles Ak, Ar, and Ap
* Green – with angles Ao, Aq, and Aj.
Expressed in ratios of sides:
Blue – with angles Ak,
Ar, and Ap
AK/BC=EK/BE=AE/CE
Green – with angles Ao,
Aq, and Aj.
AJ/CB=FA/BF=JF/FC
H'mmm – I want to find other ratios. I'd also like to be able to set some of the angles above equal to one another, but can't see it. This may be enough, so see if there is something that can be done with these given equations using algebra.
We're trying to show that AF*BD*CE = FB*DC*EA.
To help find pattern matches to our equations, it will help to rewrite them while making sure AF isn't written as FA.
Sketch 1 yielded AP/DP = JP/CP = JA/DC = KP/BP = KA/ BD.
Sketch 2 yielded KA/BC=EK/BE=EA/CE, and JA/BC=AF/FB=JF/FC
After finding the matching segments in the above equations (bolded) , it's easy to note that we want to get rid of anything that includes the ancillary construction points J, K and P.
Reviewing the equations above with the intent of using the equalities to eliminate anything with a J,K, or P in it finds the common segments from Sketch 1, JA and KA, that are mixed in with the Sketch 2 equations. Perhaps solving and substituting will work.
From Sketch 1: JA/DC = KA/BD ( this equation has the potential to tie things together if we can substitute for JA and KA with the values we want.
From Sketch 2 KA/BC =EA/CE : so KA = (EA/CE)*BC
JA/BC= AF/FB: so JA = (AF/FB)*BC
cool – both of these happen to have a common multiple of BC which may cancel out.
Sketch 1 equation is:
JA/DC = KA/BD
JA* BD = KA *DC
Substitute in Sketch 2 equalities:
(AF/FB)*BC*BD = (EA/CE)*BC*DC -The BC's cancel out
(AF/FB)*BD = (EA/CE)*DC and we want to pull divisors up.
AF*BD*CE
= EA*DC*FB
And that's the desired outcome, so all is proven.
Generalization
for P outside the triangle.
Yes – GSP proves a useful tool in proving this general case. See the fourth tab of our GSP File for a working sketch of this example.
C.
Show that when
P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?

See tab 'C' of our
GSP file. It does indeed appear that the
ratio is always greater than 4. How to
prove it I don't know yet, but the minimum does seem to occur when P is near
the center of the triangle and the maximums' when P is near the edge (so the
triangle DEF has very small area).
Speculate that the minimum occurs at one of our triangle key points (G,H,C,I) so overlay that construction.
H and are clearly
not the answer, but the Centriod G does give the
minimum ratio of 4.
The notion that the
minimum happens at the Centroid gives many clues to
the proof of this phenomenon. When P is
at the Centroid, the lines through it and the
vertices will form angle bisectors of the vertex (just as with the construction
for G). These bisectors will intersect the
opposite side at its median, thus our triangle DEF is now a medial triangle
that inherits all the properties of a medial triangle, as outlined in
Assignment 3, including:
* Sides parallel to
the 'parent' triangle.
* Sides ½ the length
of the corresponding side in the parent triangle
* And finally, it is similar to the original triangle and one-fourth of its area.
So we can see that the ration of areas is 4, but to prove that any other triangle DEF will have a higher ration (lesser area) is another matter.
After noodling,
not apparent to me. Hopefully
some of the extra work on 10,11,12 can compensate.