

First, let's see a graph of the equation: ![]()

So, when the exponent 'n' equals 2, the equation is a graph of a circle, centered around the origin.
Let's look at the graph of : ![]()
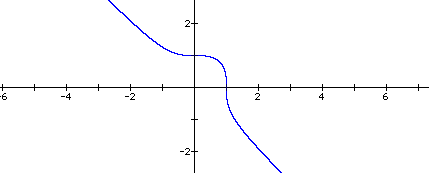
When 'n' equals 3, the equation graphs as a 'line with a bend' from approximately y = -1 to 1, around the origin.
Now I overlay the two graphs:
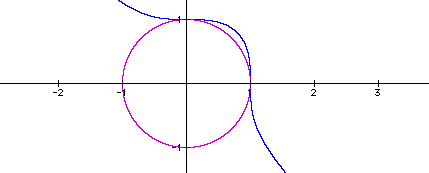
We will come back to the odd numbered exponents, but first...
What changes do we get as we increase 'n' as an even number? Let's look at n=4.
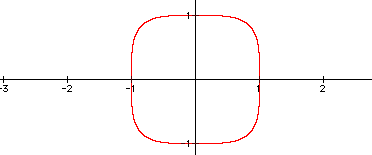
With even exponents equal to 2, the graph was a circle. With even exponents of 4, the graph starts to resemble a sort of rounded square.
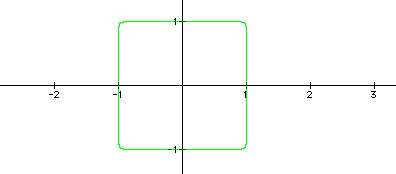
How does the graph change as we make the even exponents really large? Let n =24: Then the graph of the equation
looks much more like a square than a circle. See below.
Now let's see the progression from circle to 'square' on one graph,for even exponents equalling 2,4 and 24! click here
Now we will resume our review of the odd numbered exponent equations. Above, we looked at the equation where the exponents were equal to 3. We observed that the resulting graph was a line descending from left to right, with a bend to the right around the origin. Now let's look at the equations:
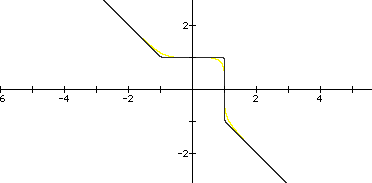
We can see that these graphs also are straight lines except around the origin, and like the equation with the exponents equal to 3, there is a bend to the right. We notice that the bend becomes more pronounced as the exponents get larger. The bend approaches a right angle at (1,1).
We can make a statement about the graphs of the even and odd exponent equations. The even numbered equations are not functions, because for some X values, there are two Y values(around the origin where the circle/square effect is). Whereas the odd numbered equations are functions because there is only one Y value for each X value, everywhere each equation is graphed.
An extension of this problem would be to analyze the equations numerically, but I have not attempted to do that in this assignment.