Assignment #2
Keith Schulte
For today's assignment, we will look at graphs of:
![]()
These graphs are parabolas that all open upward, with vertices at the origin (0,0). When a=1, the basic graph looks like this:
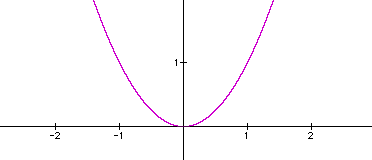
What will happen as we change the variable a? What will the graph do when we make 'a' larger than 1? What will happen when we make the 'a' some value between 0 and 1? What would happen if we make 'a' a negative number? The graphs of this equation quickly show us a pattern. So let's look at the graph of:
![]()
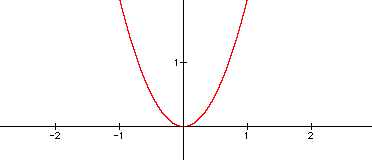
We can see that as ‘a’ goes from one to two,
the parabola rises more steeply. Therefore we would expect that as a gets ever
larger the parabola will narrow and rise even more steeply. So let’s view the graph of:
![]()
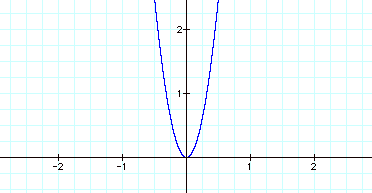
As we expected, the graph shows us a much
steeper parabola. Now, what would happen if we make ‘a’ less than one? If making
‘a’ larger makes the graph rise more steeply, then we could expect that making
‘a’ smaller would make the parabola rise less steeply. So now we look at the
graph of the equation:
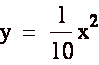
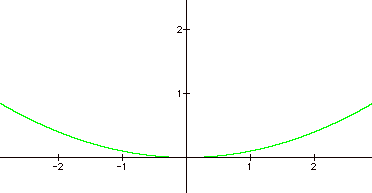
Once again, the graph is as we expected. The
parabola rises much more slowly. We have looked at positive values of ‘a’. Now
let us consider what would happen if ‘a’ is negative? Let us review the pattern
that has happened above. As positive ‘a’ gets larger the parabola rises more
sharply. When we let ‘a’ be less than one, the parabola flattened out,
approaching a straight line along the x-axis. So it would seem logical that if
we continue to make ‘a’ even smaller, i.e. a negative number, it would start to
curve the opposite way, opening downward. Let’s look at the graph of the
equation:
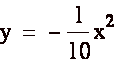
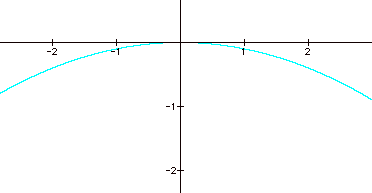
Here, we let ‘a’ equal a negative one-tenth
and it did open downward. It now appears obvious that as we let ‘a’ equal
ever-larger negative numbers, it will open downward evermore steeply. Let’s
view the graph of:
![]()
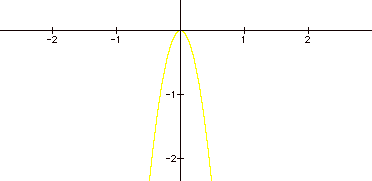
It confirms our idea that the larger negative
‘a’ would be a parabola that opens more sharply.
SUMMARY: The graphs of this function have a
predictable pattern. This set of
graphs would be good as a demonstration to a classroom of young math students.
Putting up one graph, then questioning the students about expected outcomes as
we change the value of ‘a’. After the second or third graph, the students would
likely be able to correctly say what the outcome would be of the next change in
‘a’.
