Assignment #6: Explorations with Geometer's Sketchpad
By: Keith Schulte
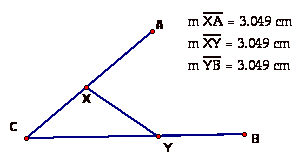
Given three points A, B,
and C. Draw a line intersecting AC in the point X and BC in the point Y such
that:
AX=XY=YB
We are given the following
figure:
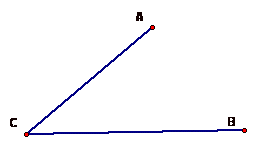
Create the segments indicated
above. One on segment AC, which will be segment XA. One on segment BC, which
will be segment YB. The third segment will connect X and Y. All three segments
must be equal.
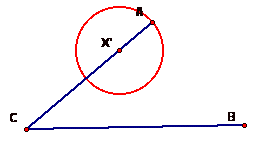
Start by selecting an
arbitrary point on segment AC. Call this point X'. Then create a segment between point X' and point A.
Select X' and the segment AX' and construct a circle by center (X') and radius
AX'.
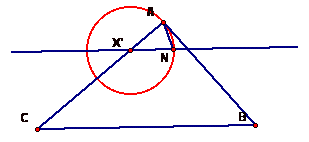
Next, construct a line
parallel to CB, through point X'. Then construct the point of intersection of
the circle and the parallel line. The point of intersection will be called N.
Then construct a segment from point A to point N. Next, construct a segment
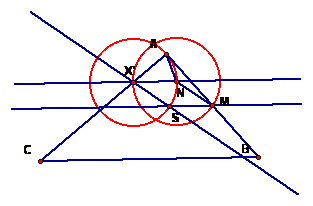
from point A to point B. The diagram now looks like this:
Using point N and segment AX',
construct a circle, by center and radius. This gives a point of intersection on
segment AB. Call the intersection point M. Construct a segment from point N to
point M. Then construct a line parallel to segment CB through point M. Now
construct a line parallel to segment NM through point X'. This creates an
intersection between the parallel line through point M, the parallel line
through X', and the first circle. Now we have:
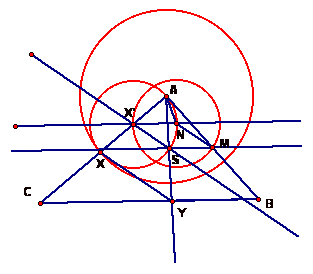
We have now completed the
preliminary construction necessary to give us our desired segments. By constructing
a ray from point A through point S, we create an intersection on segment CB.
This intersection is our desired point Y. We then create segment YB. Using point
A and segment YB, create a circle by center (A) and radius YB. This creates an
intersection on segment AC which is our desired point X. The last step is to
create a segment between points X and Y.
Geometer's Sketchpad has a
function allowing us to measure the three segments. This is not 'proof' that we created the sketch
correctly, but if the segment measurements aren't the same, then we know we did
not correctly complete the sketch. Below is the final construction with the
preliminary construction elements hidden.