
Assignment #8: Altitudes and Orthocenters
By: Keith Schulte
We will start our exploration of Altitudes and Orthocenters by constructing a triangle ABC and it’s Orthocenter H. Remember the Orthocenter of a triangle is the intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the opposite side of the triangle.
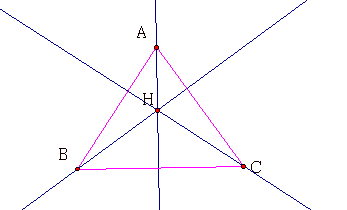
By constructing the orthocenter of the triangle above, we can consider the triangles HBC, HAB and HAC and each of their Orthocenters. Our next GSP sketch includes triangle HBC and it’s orthocenter.
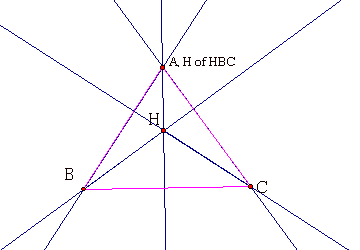
From our GSP sketch (using a script tool to create the orthocenter), we can see that the orthocenter of triangle HBC is at the same point as point A of triangle ABC. It is on the altitude from vertex H of triangle HBC. Knowing that, where would we expect the orthocenter of triangle HAB to be? The altitude of triangle HAB that goes through vertex H also goes through point C of triangle ABC. So our conjecture would be that point C would be the Orthocenter of triangle HAB. Let’s see if we’re correct!
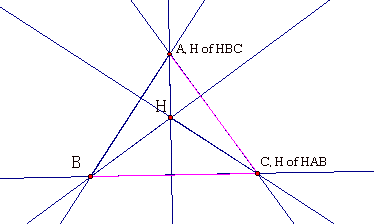
Yes, we were right! So we can predict that the orthocenter of triangle HAC will be at point B of triangle ABC, because the altitude, intersecting vertex H of HAC also goes through point B. You can check this out by clicking HERE to use my toolfolder. Use my Orthocenter script tool to recreate what we have done above and to create the orthocenter H of triangle HAC. Do you find that point B is the orthocenter?
Now we will create the Circumcirles of the four triangles ABC, HBC, HAB and HAC. The center of a circumcircle, the circumcenter, is a point equidistant from the three vertices. Since the center is equidistant from the three vertices, the vertices are points on the circumcircle.
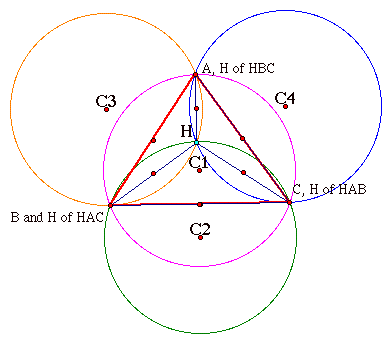
Since the vertices are points on the circumcircle, we can tell from the GSP sketch above that the fuchsia colored circumcircle is the circumcircle of the original triangle ABC, with circumcenter C1. We know this because all three of triangle ABC’s vertices are points on the circle. No other triangle in our sketch has three vertices as points on this circle. Likewise, the green circle is the circumcircle of HBC, with circumcenter C2. The orange circle is the circumcircle of triangle HAB, with circumcenter C3. The blue circle is the circumcircle of HAC, with circumcenter C4.
Are there any relationships between each of the four Circumcenters and the points A, B and C? If we create segments connecting each point. We find that a cube is constructed connecting all of these points. What does that indicate? If it is a cube, then each point is equidistant. We can strengthen this conjecture by measuring the distant between several of these points. If all the segments tested are the same distance, it supports our idea. Let’s look at the sketch:
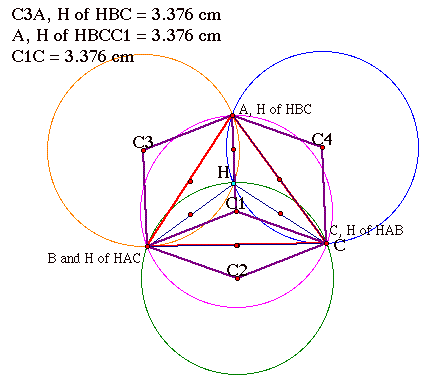
The three arbitrarily selected segments (C3A, AC1 and C1C) all have the same measurements. We would find that the other three are also the same length. Therefore, all of the six triangles created are similar.
Now let’s explore a little further. What would happen if we moved any of triangle ABC’s vertices to where the orthocenter H is located? We would start with the following sketch:
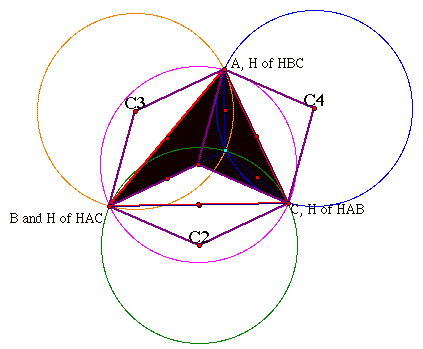
So what would happen if we moved vertex A to where orthocenter H is? Where would the orthocenter H move to? Here is a picture of moving point A to point H. Also below, I have included a link to my toolfolder.
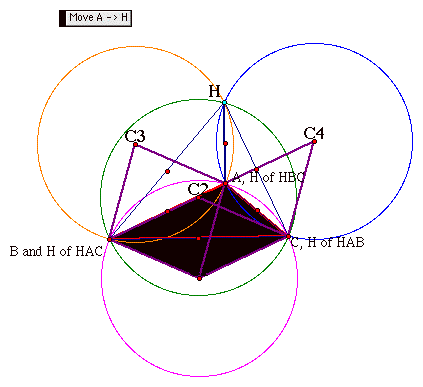
When we compare the before and after sketch, we notice that when we move point A to where point H was, Point H moved to where point A had been. Notice also that the green and fuchsia circumcircles have changed places. Also, C1 and C2 have switched places. If we moved point B or C to where point H was, we could foresee similar results.
Click HERE to go to my toolfolder (only works if you have GSP on the computer you are working on). You will see a blank screen. When GSP opens, a toolbox will be on the left side. Click on the last icon (the arrow and three dots). Under ‘This Document’, select A8MoveVerticestoH and you will be able to explore more. Have fun!