
Assignment #9 Pedal Triangles
By: Keith Schulte
What is a Pedal Triangle? We need to start with a given triangle ABC. Then we pick any point P in the plane. We then construct a perpendicular line through P and each side of triangle ABC. Each point where the perpendicular lines intersect a side of the triangle ABC (or lines extended from each side) is a vertex of the Pedal Triangle. Below is a Geometer’s Sketch Pad (GSP) sketch of one pedal triangle (the orange triangle), when P is in the interior of triangle ABC.
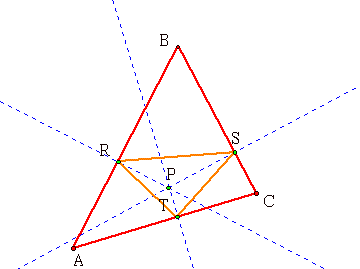
Since the pedal point can be any point in the plane, we can consider many possibilities. The pedal point P may be outside of triangle ABC. What would the pedal triangle look like then? Would the pedal triangle be entirely inside the original triangle ABC? Would the pedal point be on the interior of triangle ABC or on the outside? Let’s look at a different triangle ABC and a different pedal point, on the exterior of triangle ABC.
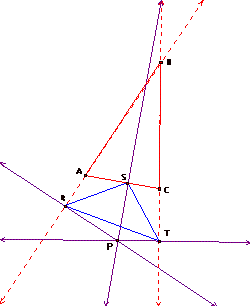
In the GSP diagram above, the original triangle is triangle ABC and our pedal point P is at the bottom of the diagram, outside of the original; triangle. When we draw the perpendicular lines to each side, we find that two of the perpendicular lines (the purple lines) do not intersect the sides of the original triangle. So we extend these two sides of the triangle (the dashed red lines). Where each extended side is intersected by the perpendicular line from the pedal point P, is a vertex of our pedal triangle RST. So when we extend segment BC, the perpendicular to segment BC from P is at point T.
Notice that in this scenario, the pedal triangle is outside of the original triangle and the pedal point is outside of both the pedal triangle and the original triangle.
We have previously considered several centers of triangles. The pedal point P could be one of these centers, for example, it could be the incenter. What is the definition of an incenter? Who can tell me how we can create the incenter?
Remember that the incenter is a point on the interior of the triangle that is equidistant from the three sides. An interior point that is equidistant from the two sides of an angle lies on the angle bisector. So, the incenter ‘I’ is on the angle bisector of each angle of the triangle. So let’s create a triangle with an incenter and let the incenter be the pedal point.
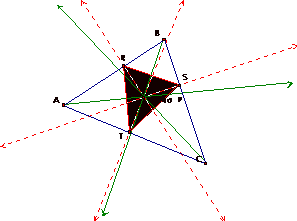
In the sketch above, the rays (in green) are the angle bisectors. The red dashed lines are the perpendiculars from I to each side of the triangle. Therefore, the incenter and the pedal point are the same. The incenter is always on the inside of the original triangle and so when P and I are the same, P will always be on the interior of triangle
So, we’ve seen that the pedal point can be inside or outside the original triangle. The pedal triangle can be inside or outside the original triangle. The pedal point can also be a point on the original triangle, on a side or at a vertex. Let’s look at a sketch when the pedal point is on a side of the original triangle. It would look like this:
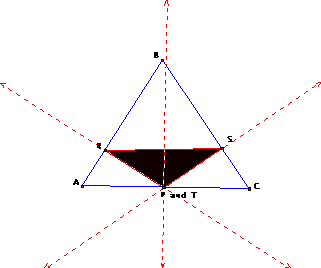
Open up my GSP toolfolder by clicking HERE. It opens a blank GSP sketch. On the left will be a control panel, which is called the toolbox. When you have my toolfolder open, you can click on the last option in the toolbox (the arrow and 3 dots) and select the pedaltriangleks option. After you create a triangle with the tool, click somewhere in the document to place your pedal point, After you’ve practiced a little, then you can see if you can create a pedal triangle with the pedal point on one of the sides of the original triangle and the pedal triangle not be inscribed inside the original triangle. Try a pedal point at a vertex, what does the pedal triangle look like? Is this a special situation? If yes, what kind of special triangle do you get? There are many other explorations. So explore! Have fun and see what you find!