
Final Project Summer 2003
Triangle Ratios
By: Keith Schulte
Part One:
I have reviewed projects 1 through 12 and have completed my revisions.
Part Two, A
The problem is to consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP and CP extended to their intersections with the opposite sides in points D, E, and F respectively. One such triangle would look like this:
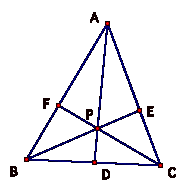
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
The triangle above is a random triangle with a random point P. WeÕll look at this triangle as our first example and then try some other various triangles and various points P. So, in GSP, I will create the segments and then measure each segment. I will then use the calculator to multiply (AF)(BD)(EC) and (FB)(DC)(EA). We will see if see a relationship.
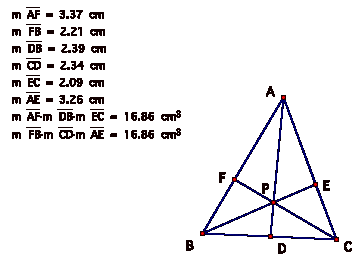
For this random triangle and point P, we find that the products of the segments are equal. By exploring some more, letÕs see if we can assert that the products of these segments are always equal or if we find some other pattern.
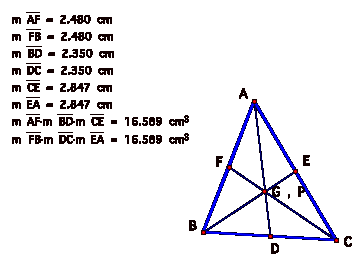
Next, letÕs look at an acute triangle with point P as the CENTROID of the
triangle and see what the result is! We know that when P is the centroid, that points D, E, and F are at the midpoints of segments BC, AC and AB. Each of our products is going to have an equal measure from each side of the triangle. So once again we will find that the products are equal. HereÕs the GSP sketch with the measurements:
What if we try an acute triangle with point P as the ORTHOCENTER? Will we find that the products are again equal? HereÕs a GSP sketch. I start with an acute triangle from my toolfolder and then overlay an orthocenter on it and label the triangle and the orthocenter as H & P. HereÕs the sketch:
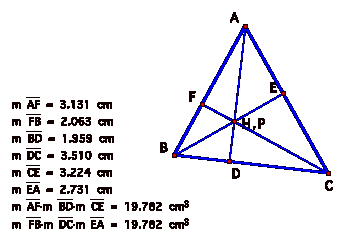
Once again, the products are equal. LetÕs try P as the INCENTER, and see if the products are equal for an acute triangle:
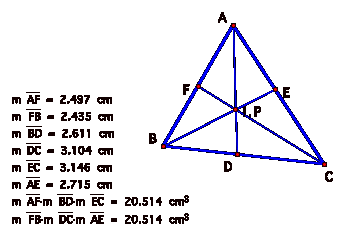
So for all of the acute triangles and different placements of P above, we see that the products of the segments (AF)(BD)(EC) and (FB)(DC)(EA) are equal. LetÕs see if this happens for some right triangles. First weÕll try a right triangle with a random point P:
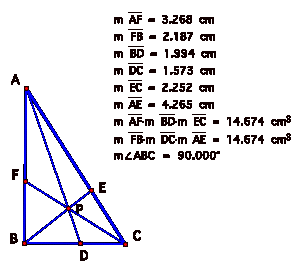
Once again, the products are equal. We know that if we try a right triangle and have point P be the CENTROID of triangle ABC, that we will find that the products are equal. What if we let P be the INCENTER of a right triangle? Will the products be equal? HereÕs the sketch:
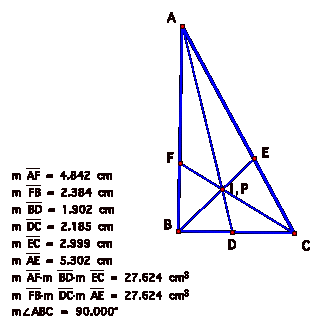
Once again, the products are equal.
Will we get the same results if we look at an obtuse triangle with a random point P on the interior?
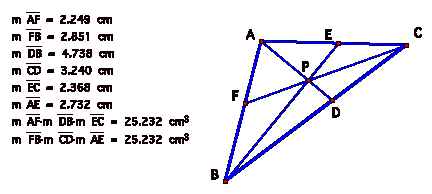
So, for this obtuse triangle, the products of the segments (AF)(BD)(EC) and (FB)(DC)(EA) are equal.
LetÕs try one more obtuse triangle, with P as the Orthocenter.
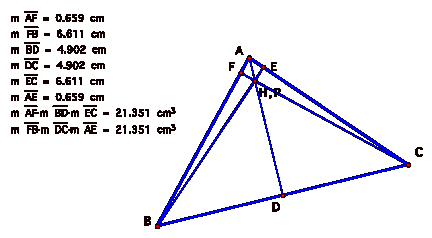
Once again, the products of the segments is equal. So, in all the cases above, when P is a point within triangle ABC, the products of the segments (AF)(BD)(EC) and (FB)(DC)(EA) are equal.
Part Two B:
From Part A, we establish the conjecture that for any triangle ABC with point P a point inside the triangle and lines drawn from the vertices and through point P to their intersection on the opposite side of the triangle in points D, E, and F, then the products of the segments (AF)(BD)(EC) and (FB)(DC)(EA) are equal. Now for part B, we need to prove it!
If (AF)(BD)(EC)=(FB)(DC)(EA), then if we divide both sides of the equation by (FB)(DC)(EA), we would have:
|
(AF)(BD)(CE) |
= 1 |
|
(FB)(DC)(EA) |
So, what is required is a proof of CevaÕs Theorem. From Dr. WilsonÕs write-up on CevaÕs Theorem, the theorem states that: Ņthe product of the ratios of the pairs of segments formed on each side of the triangle by the intersection point is equal to 1, where the ratios are taken in the same orientation on each side. Further, if the ratio formed by any three Cevians is equal to 1, then the three Cevians are concurrent.Ó Concurrence means they intersect in one point.
So we are given triangle ABC and a random point P. We draw lines from each vertex, A,B, and C, through P and extend each line to their intersections with the opposite sides to points D, E, and F, respectively. These lines through P are the Cevians.
From part 2 A, by reviewing many GSP sketches of these segments, we arrived at the conjecture that (AF)(BD)(EC) = (FB)(DC)(EA). Then by dividing both sides of the equation by the right side of the equation, we arrived at the ratio of the products being equal to 1.
So, we need to prove this! I wasnÕt sure how to proceed, other than I knew that Dr. Wilson had indicated that we would nee to create some similar triangles. I found a very good illustration of how CevaÕs Theorem is proven at http://www.cut-the-knot.org/Generalization/ceva.shtml. I applied their method to our slightly different information. Below is a GSP sketch with the given information and the lines through P extended. Then I add a line parallel to BC, through point A. The point where the extended segment CF intersects the parallel line, we label point H. The point where the extended segment BE intersects the parallel line, we label point G. So here is the sketch:
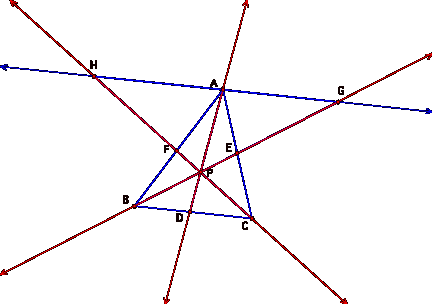
Line HG is parallel to BC. Therefore, we have the following pairs of similar triangles:
1) AFH and BFC
2) AGE and CBE
3) AGP and DBP
4) AHP and DCP
In 1, above angle A is equal to angle B. because segment AB is a transversal, which intersects two parallel lines. This creates alternate interior angles. For the same reason (with HC being the transversal), angle H is equal to angle C. Also, angle AFH and angle BFC are alternate angles and thus equal.
From these similar triangles, we can derive the following ratios, because if triangles are similar then corresponding sides of those triangles are similar:
1) AF/FB = AH/BC
2) CE/EA = BC/AG
3) AG/BD = AP/DP
4) AH/CD = AP/DP
By substitution, from ratios 3 and 4, we have AH/CD = AG/BD. Also from 3 and 4, we can say that CD/BD = AH/AG. Therefore, we can rewrite the equation:
|
(AF)(BD)(CE) |
= 1 |
|
(FB)(DC)(EA) |
As the following:
|
(AF)(BD)(CE) |
= |
(AH)(AG)(BC) |
|
(FB)(DC)(EA) |
(BC)(AH)(AG) |
Then on the right side of the equation, we can see that each product in the numerator is also in the denominator and thus each cancels out and leaves us with 1 on the right side of the equation. Thus we have proven that the product of the ratios on the left side do equal 1. The proof of CevaÕs Theorem also says that the fact that three lines intersect at one point is enough for the first equation above to be true.
Now to show that we can generalize the result above, that the point P can be outside the triangle.
Go to my toolfolder, by clicking HERE and open the tool named Final Project Š Part B#2 and you can see that if we move P outside of the triangle, that we can still find similar triangles. When you open the tool, start by creating a triangle, then a point inside the triangle, then select a point somewhere close to, but outside of the triange, then click on the move button. The points of the cevians move, but they are still concurrent, so we see that we can have point P outside of the triangle. The point in the center of the triangle is point P (although GSP would not allow me to label it in my tool). Also, GSP would not allow me to label the points of the triangle. So one should label these points before animating the motion of P from inside the triangle to the outside (point A, is at the top of the triangle, point B is at the bottom left and point C at the bottom right, and point P inside the circle).
PART C:
Show that when P is inside the triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
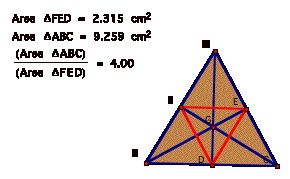
When P is the centroid G, then the ratio of the areas of the triangles is equal to 4.
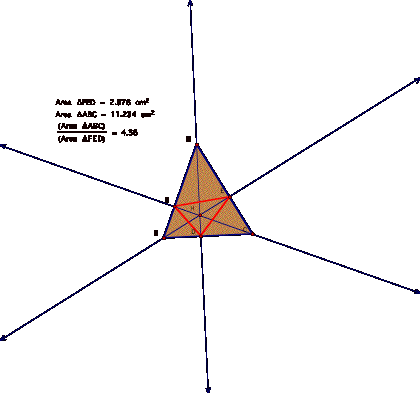
When P is the Orthocenter, then the ratio of the triangles is greater than 4! As illustrated below.
When point P is the Incenter, then the ratio is also greater than 4 as shown below!
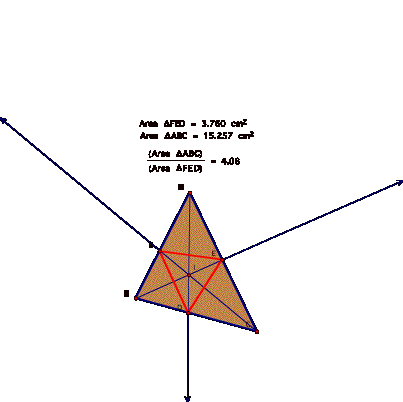
If the smaller triangle is the pedal triangle, then the ratio of the areas is again larger than 4 as seen below.
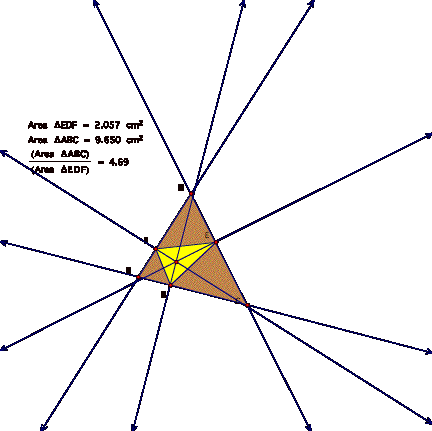
So, in all cases I tried, the area of the larger triangle is always more than 4, except when P is the centroid, then the ratio is equal to four.