

Title: Investigations into the angle Bisectors of a Triangle
Problem Statement: Prove that the three angle bisectors of the internal angles of a triangle are concurrent.
Problem Setup: The problem is intended to prove that the three angle bisectors of the internal angles of a triangle all go through the incenter of a triangle. If all three angle bisectors of the internal angles go through the same point then they are necessarily concurrent.
Plans to Solve/ Investigate the Problem: I plan to use gsp to show that two angle bisectors of a triangle will form congruent triangles and then use congruent parts of congruent triangles are congruent to show that a third angle bisector of the angle whose vertex is the intersection of the angle bisectors of two of the internal angles of the triangle must be the angle bisector of the other side. By showing this I will prove that the three angle bisectors of the internal angles of a triangle are concurrent.
Investigation/ Exploration of the Problem:
I began by constructing a triangle.
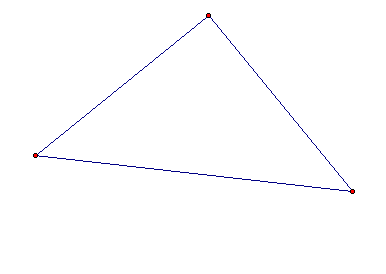
I then constructed two of the three angle bisectors for two of the internal angles of the triangle.
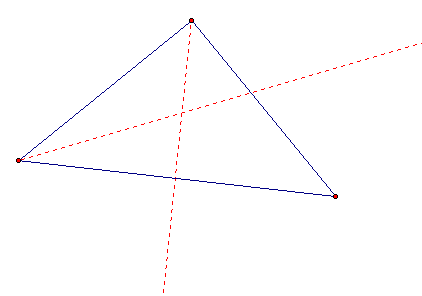
Next, I constructed the intersection of the two angle bisectors.
Then I constructd perpendicular lines from the intersection point to each of the three sides of the triangle.
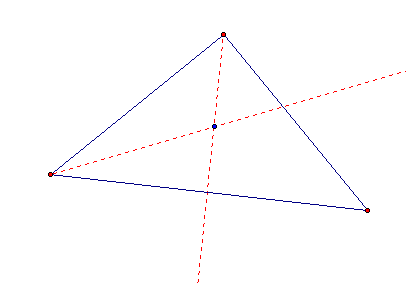
Next, I constructed the intersection of the perpendicular line segments that I constructed and the three sides of the triangle.
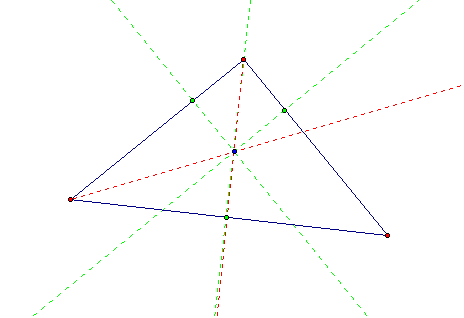
I then constructed the segments from the intersection of the two angle bisectors (in blue) to the intersection of the three perpendicular lines with the sides of the triangle (in green).
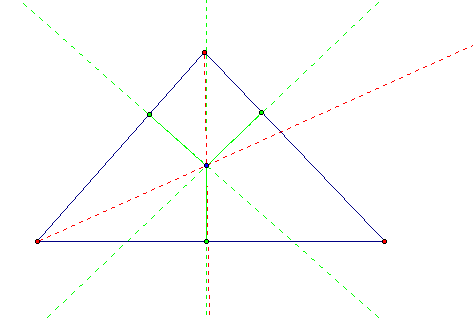
I then proceeded to hide perpendicular lines.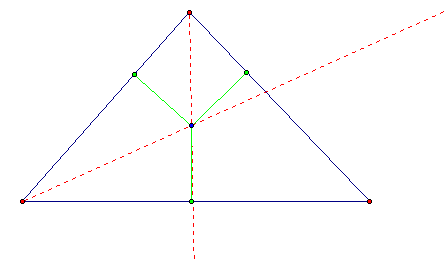
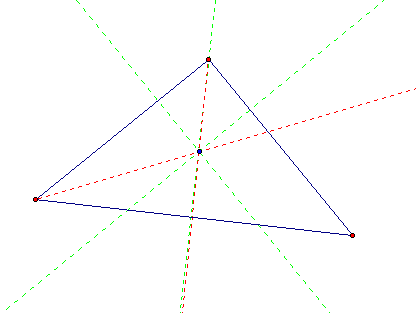
I then constructed a circle whose center was the intersection of the two angle bisectors and whose radius was the length of the perpendicular segment I created.
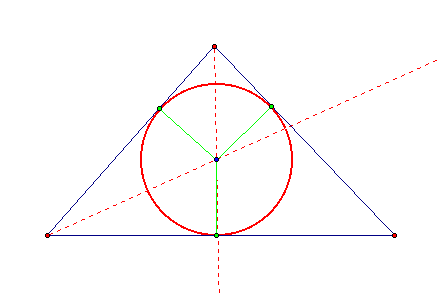
Notice that this circle is inscribed inside of my triangle. I then construct the angle bisector of the angle whose vertex is the intersection of the two angle bisectors of two internal angles of my triangle.
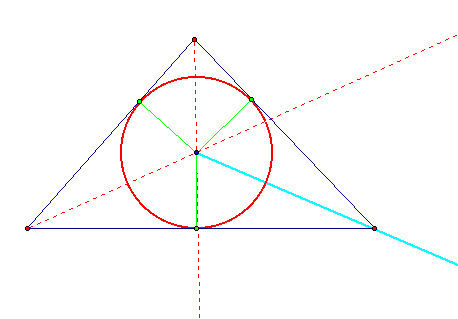
Notice that the angle bisector of this point goes through the third side of the triangle. How can I show that this indeed forms the angle bisector of the third internal angle of my triangle?
Look at the two triangles that I have formed in the construction:
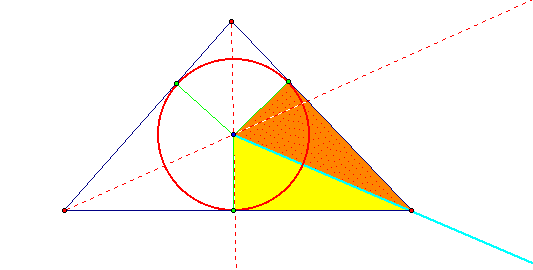
Notice that these two triangles must be congruent by the SAS Theorem. The radii of a circle are always congruent so in this case the sides of my triangles that are both radii of my inscribed circle are congruent. Also since I constructed the angle bisector of the angle formed by the intersection of two of the angle bisectors of two of the internal angles, those two angles are congruent. Also the two triangles share a common side so they are congruent by the reflexive property. Therefore the two triangles are congruent by SAS. Since the two triangles are congruent I know that the two angles of the triangles formed at the vertex of my triangle must also be congruent by CPCTC. Therefore the light blue line is the angle bisector of the third internal angle of the triangle. This must go through the intersection of the other two angle bisectors of the internal angles of a triangle because the vertex of the angle we used to create the light blue line was this intersection. Therefore the three angle bisectors of the three internal angles of a triangle must intersect. Therefore, these three angle bisectors must be concurrent, since concurrent lines are three or more lines that intersect. Their point of intersection is called the incenter of the triangle.
Extensions of the Problem: There are several options for extending this problem. One can prove that the three angle bisectors of the three internal angles of a triangle are concurrent algebraically. One can also prove why the three altitudes of a triangle are concurrent or why the three centroids of a triangle are concurrent. To extend this problem I am going to prove that the angle bisectors of the internal angles of a triangle are concurrent algebraically.
I will begin by labeling the sides and coordinates of my triangle:
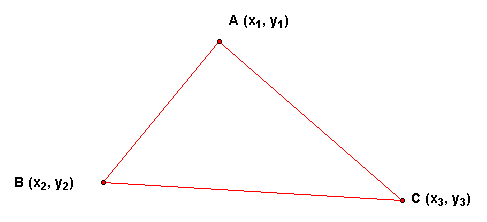
I then note that the internal bisector of <A meets the side BC pt. D and that the internal bisector of <A and <B meet at point I:
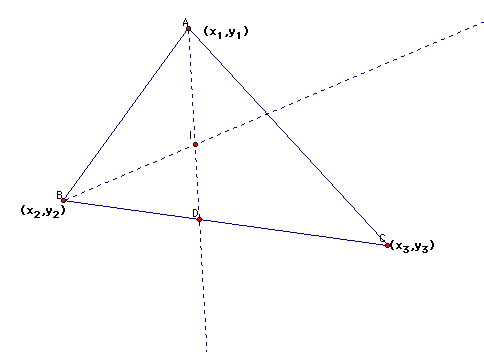
In this case BD/DC = AB/AC. One can then look at the section formula. The section formula is stated as follows: P(x,y) and Q(x,y) are two points in a coordinate plane. Let R(x,y) be the point which divides [PQ] internally in the ratio of :
so that :
Then the coordinates of R are as follows:
So in the case of my triangle using the section formula the coordinates of my incenter are:
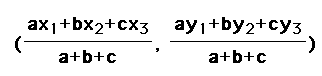
Because these coordinates are symmetric the incenter must lie on the bisector of angle C. Therefore the internal bisectors of the internal angles of a triangle are concurrent.
Links:
Jennifer Shea