

Problem Statement: Construct a parabola:
a) Using an action button to generate a parabola from the animation and trace of a constructed point
b) By constructing the locus
c) Repeat the construction of a) with a trace of the tangent line
Problem Setup: In going through the steps of the constructions of a parabola, I intend to investigate the properties of a parabola and the reasons why the constructions of a parabola can be done in these particuar ways.
Investigation/ Exploration of the Problem:
I will begin by constructing a parabola using an action button to generate a parabola from the animation and trace of a constructed point.
I begin my construction with a line and a point not on the line. A parabola is a set of points equidistant from a line called the directrix and a fixed point called the focus. So, at the beginning I am constructing the directrix and the focus of my parabola.

For the next part of the construction it is useful to investigate the following equation:
In this equation if I set 4p = a, being the number in front of the:
In the standard form of the equation:
p is equivalent to the distance from the vertex to the parabola. Since, as was already noted, a parabola is the set of points equidistant from a line and a fixed point, p also represents the distance from the vertex of the parabola to the directrix (line). This is the reason for the next part of the construction. The next part of the construction involves choosing an arbitrary point, which I called point C, on the constructed line, line AB. I then constructed a perpendicular to line AB through my point C. Next, I constructed the segment from pt. C to my focus, which I called pt. D. I then took the midpoint of segment CD and called the midpoint E. I then constructed the perpendicular line to segment DC through E. This process of construction forms an isosceles triangle. In this isosceles triangle the length of the two isosceles sides of the triangle is equivalent to p and the two congruent sides of the isosceles triangle are equidistant from point D, the focus and line AB, the directerix.
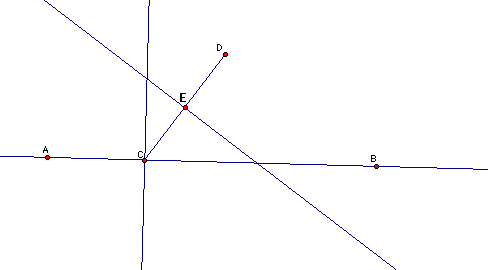
The length of segment EC and segment DE should be equivalent.
I now construct F which is the intersection of my two perpendicular lines.
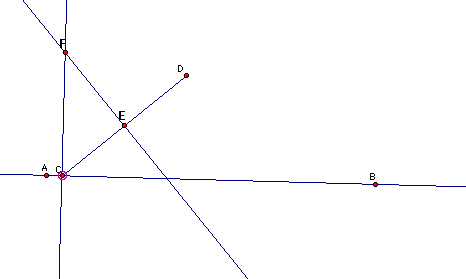
As I animate point C bidirectionally along line AB and as I trace pt. F, I obtain a parabola.
Click HERE to see the animation.
We have already discussed the idea that a parabola is the set of points equidistant from a line (the directerix) and a given point (the focus). This means that the locus of points equidistant from a line and a given point is a parabola. So I can also construct my parabola by the locus. If I select point F and pt. C and construct the locus I obtain the parabola. Pt. E is the point, which is equidistant from line AB and the focus D. So, as I move point C bidirectionally along line AB point F moves along line EF. At Every point F is equidistant from pt. D (the focus) and line AB (the directerix), because it is perpendicular through line E.
Click HERE to see the construction of the parabola with the locus.
One can see the set of triangles that are formed as C is animated along line AB. Notice that as one approaches the vertex of the parabola, the triangle appears to shrink to a straight line. The set of isosceles triangles that are formed shows that every point on the parabola is equidistant from the focus D and the line AB.
Click HERE to see this animation.
By constructing two circles, one with center C and radius length equivalent to segment CF and the other with center D, and radius CF, I can see that as C is animated along line AB the circles always intersect at line F. Since the radii of my two circles are the same I know that the distance from segment DF must be equivalent to segment CF. Further verifying my construction of a parabola.
Click HERE to see this animation.
I can also trace the tangent line to see the construction of the parabola. The trace of the tangent line will envelope a parabola.
Click HERE to see the animation of the tangent line.
This is my investigation of the construction of a parabola.
Author & Contact:
Jennifer Shea