

Purpose: The purpose of this write-up is to investigate the loci of several points and lines for tangent circles.
Investigation/ Exploration:
I began my investigation by looking at the following two circles:
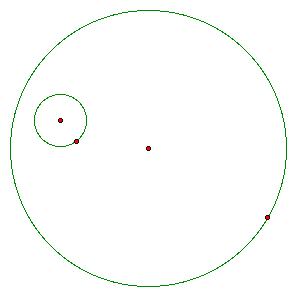
My goal was to construct a circle tangent to the two given circles. The pedagogical implications and benefits of gsp in this particular situation is that the construction is much faster and I can use the sketch pad to see step by step why the circle tangent to the two circles woud be constructed the way it is. GSP helps a student visualize the situation and explore different possibilities.
The construction of the tangent circle begins as so:
I begin by choosing an arbitrary point on the circle and construct a line through that point and the center of my larger circle. Here is the next step of the construction:
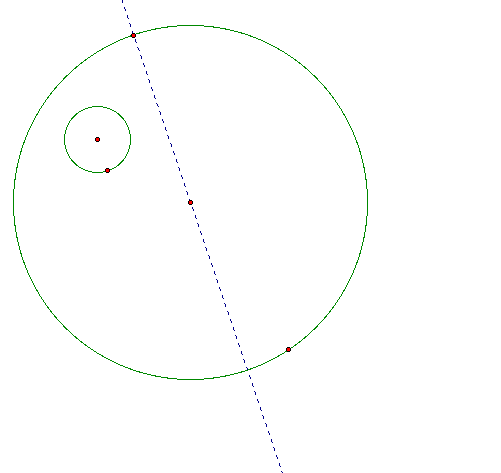
Then, I construct the radius of the small circle. I then construct a circle with center as my arbitrary point and the radius as the length of the smaller circle. I then construct the far intersection of the newly constructed circle and the line through the center of my circle. The construction of the circle is done this way because the radius of the center of my tangent circle must be equidistant from the edges of the to circles. If I take the segement from the center of my small circle and to the far intersection of my new circle I form the base of an isosceles triangle, this enables me to form a point that will be equidistant from the two circles.
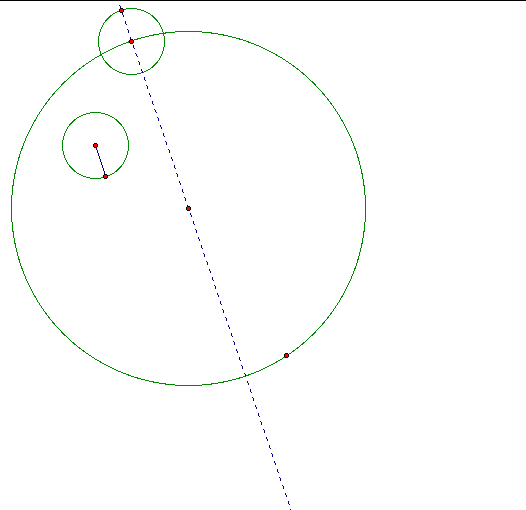
After I construct the segment from the center of my small circle to the far intersection of my newly constructed I construct the midpoint of the base of the isoscelse triangle that I have formed. I then construct a perpendicular through that midpoint and the intersection of the line through the center of my large circle. This becomes the center of my tangent circle.

All I have to do then is construct a circle, by this intersection (my center) and point (my arbitrary point on the larger circle in my given construction.
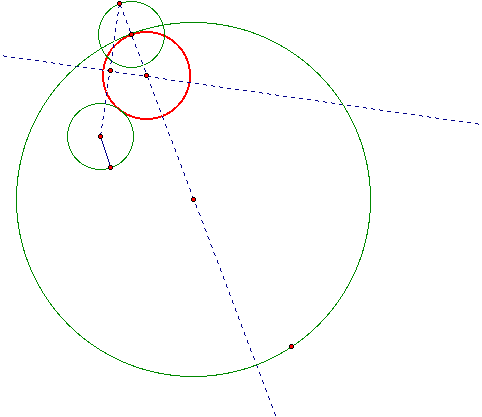
Notice that constucting the midpoint of the base of my isoceles triangle, the line perpendicular to the midpoint and the intersection of the line through the center of my large given circle and the perpendicular line gives me two congruent triangles by the Hypotenuse Leg Theorem.
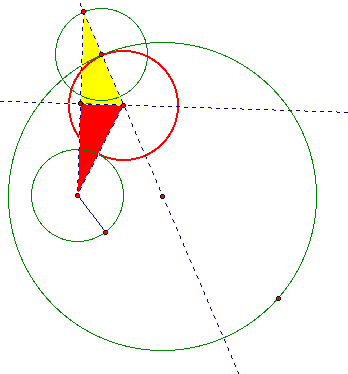
Now that I know how to do the construction my next step is to use this construction to investigate the loci that several key points and lines of this construction produce.
The first locus that I chose to investigate was the locus of the center of my tangent circle.
Notice that this produces an ellipse. Notice that pedagoically one can tie the definition of the ellipse to the geometric representation one sees here. An ellipse occurs when the sum of the distances from two fixed points is a constant. If one looks at the distances from the center of my tangent circle to the centers of my two given circles I can see as I animate the arbitrary point on my large circle to produce the tangent circle at every point from my large circle in this construction that the sum of the distances stays constant.
Click HERE to see this animation.
Now notice what happens when I trace the line in my construction that goes through the center of my tangent point. The envelope of these lines produces the ellipse. This line is tangent to the ellipse at every point around the ellipse.
Click HERE to see this animation.
The next locus I chose to investigate was the midpoint of the base of my isoceles triangle.
The trace of the midpoint of the base of my isoceles triangle forms a circle that is tangent to the ellipse at two points along the major axis of the ellipse formed by tracing the center of my tangent circle.
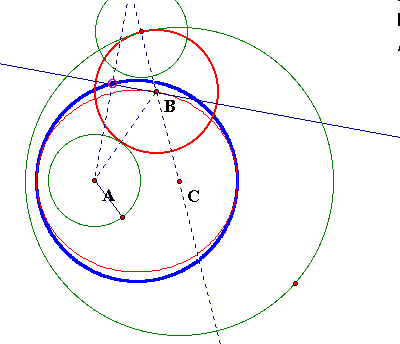
Now why is this the case?
The defintion of a circle is the locus of all points equidistant from a central point.
Click HERE to see this animation. The midpoint of the base of the isoceles triangle is equidistant from the center of my ellipse. This is why the circle formed is tangent to the circle along the two major axes.
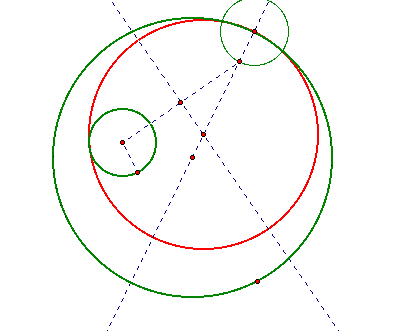
Notice that if I change the size and position of the two circles so that they come close to being tangent the ellipse in the center of the circle is is lengthed until it appears to come to a straight segment. Then as the two circles are seperated completely the locus of the center of my tangent circle is no longer an ellipse, but becomes a hyperbola while locus of the midpoint of the base of the isoceles triangle used in the construction remains a circle.
A hyperbola occurs when the differences from two fixed points, the foci, is a constant. Notice that if I measure the distance of the absolute value of the differences from the center of my tangent circle to the center of my two given circles, I obtain a fixed constant difference. Also notice that the circle which is the locus of the midpoint of the base of my isosceles triangle has a center equidistant from the two vertices of the hyperbola and is tangent to the hyperbola.
Click HERE to see this animation.
There is another construction which creates a circle tangent to two given circles and is very similar to the first construction I did. It places the tangent circle on the outside of one of my circles instead of inbetween the two given circles.
Now It is important to investigate the loci of this set of tangent circles as well. In order to make it so that one can investigate this set of tangent circles and the other set of tangent circles together I have created a script tool for both sets of tangent circles.
Click HERE to see a script tool with the script for the two tangent circles to two given circles.
This script tool allows me to move theese two circles around and investigate relationships between the two sets of tangent circles.
I began by investigating the locus of the centers of both tangent circles when one circle is inside of the other.
My picture looks like this:
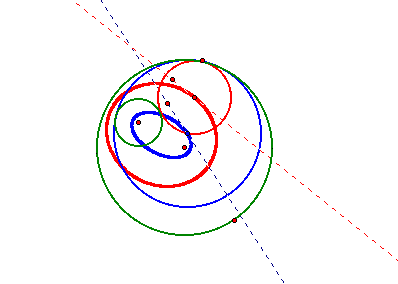
Notice that the center of my blue tangent circle traces an ellipse that is smaller than the ellipse formed by tracing the center of my red circle.
Click HERE to see the animation as an arbitrary point on this circle.
Notice that the ellipse formed by the center of my two circles a constant of the sum of the distances from two fixed points, or the foci of the ellipse.
Notice also that if I trace the midpoints of the bases of my two isosceles triangles I obtain two circles tangent to the respective ellipses.
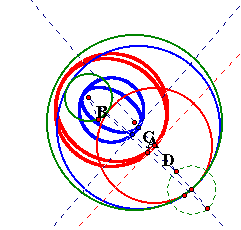
Notice that these two circles appear to be concentric circles.
Recall that before I mentioned that the center of the circle I created by tracing the base of my isoceles triangle was the center of the ellipse. This holds for both cases so that the center of both ellipses formed is the same. Since the center of these two given circles are the same this must mean that the two circles formed are concentric circles.
Click HERE to see this animation.
Now, what happens if I move the two given circles to a point where they are tangent.
Notice that at this point the locus of the center of my blue tangent circle has already formed a hyperbola whereas the locus of the center of my red tangent circle is collapsing to an straight line. Also notice that the locus of the midpoint of the base of my isosceles triangle used to construct my red tangent circle appears to be a circle that goes through the center of the two given circles.
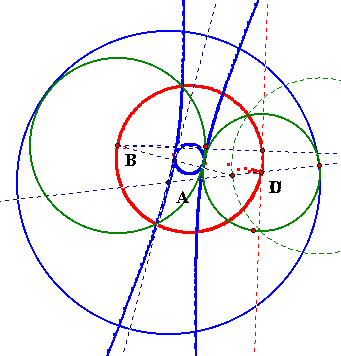
Click HERE to see this animation.
Note that the reason for these differences has to do with how the two different tangent circles are constructed.
Notice that the locus of the center of my blue circle appears to collapse to a segment when one of my circles is tangent to the other on the inside of my given circle. Or this picture looks like so:
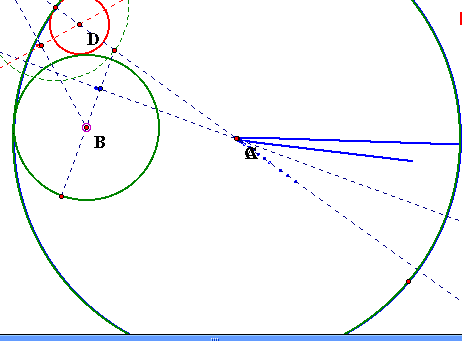
Notice that when this happens the locus of the midpoint of the base of my isoceles triangle that forms my blue tangent circle appears to go through the centers of my two given circles also notice that the locus of this midpoint of the base of this isoceles triangle also appears to be tangent to the locus of the center of my red tangent circle at two given points on the minor axis of my ellipse.

Notice that when the two circles are once again separated from one another hyperbolas and concentric circles are the loci of the centers of the two given tangent circles and the midpoints of the bases of the two isoceles triangles used to make my construction.
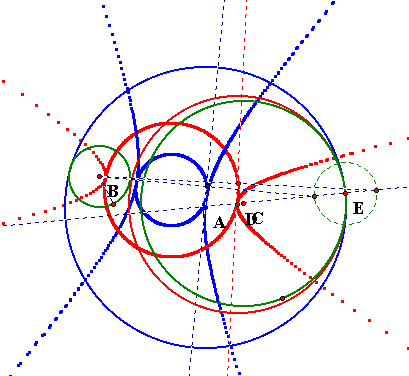
Click HERE to see this animation.
Note, that pedagogically these graphs and the locii of these graphs allows students to understand the definitions of the ellipse, the circle, and the hyperbola. This can be used to show students that these definitions really do come from geometric representions and are not just equations and definitions pulled from anywhere. This is my investigation of tangent circles and their loci in gsp.
Author & Contact:
Jennifer Shea