

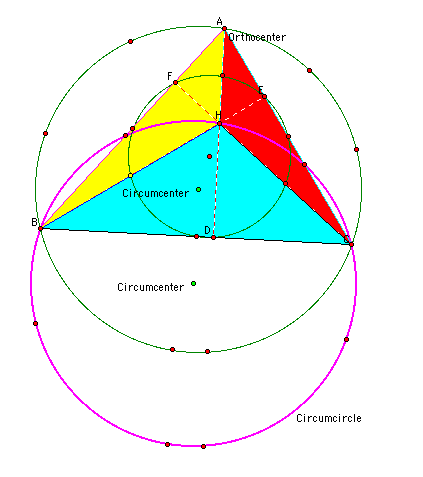
Problem Statement: Given a triangle, triangle ABC, construct the orthocenter H. Let D, E, and F be the feet of the perpendiculars from A, B, and C.
Prove:
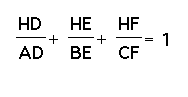
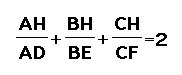
Problem Setup: I began by constructing Triangle ABC and the orthocenter, H, of Triangle ABC. I then constructed the orthcenters of Triangles HAB, HAC, and HAC. I also constructed the circumcircles of Triangles ABC, HBC, HAB, and HAC. I then used these constructions to investigate relationships to prove that:
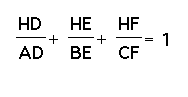
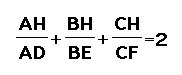
Investigations/Explorations of the Problem: I begin by constructing an acute triangle ABC and its orthocenter. The orthocenter of a triangle is the intersection of its altitudes. The orthocenter by convention is labeled H. I labeled the intersection of the sides of my triangles and the feet of the perpendiulars dropped from the vertices as D, E, F.
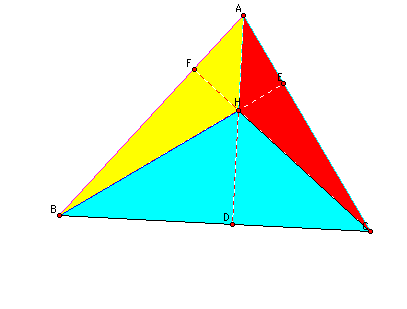
Notice that I now have several small traingles inside of my large triangle, Triangle ABC. I have triangle HBC, triangle HAC, and triangle HAB:
I then determined to find the orthocenters of Triangles HBC, HAB, and HAC. Here is the construction for the orthocenter of Triangle HBC:
Notice that the blue altitudes of triangle HBC seem to intersect at point A, indicating that A is the orthocenter of Triangle HBC.
Next, I determined to find the orthocenter of Triangle HAB. In order to do this I hid my blue altitudes for Triangle HBC and constructed segments BE, AD, and CF and hid those perpendicular lines. This was so that the construction would be easier to see, note that the orthocenter of Triangle HAB is point C.
At this point I can conjecture that the orthocenter of Triangle HAC will be point B.
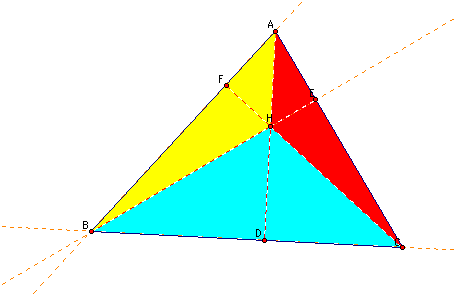
As you can see this conjecture is correct.
The next thing that I did was construct the circumcircles for triangles ABC, HBC, HAB, and HAC. This is what the construction looks like:
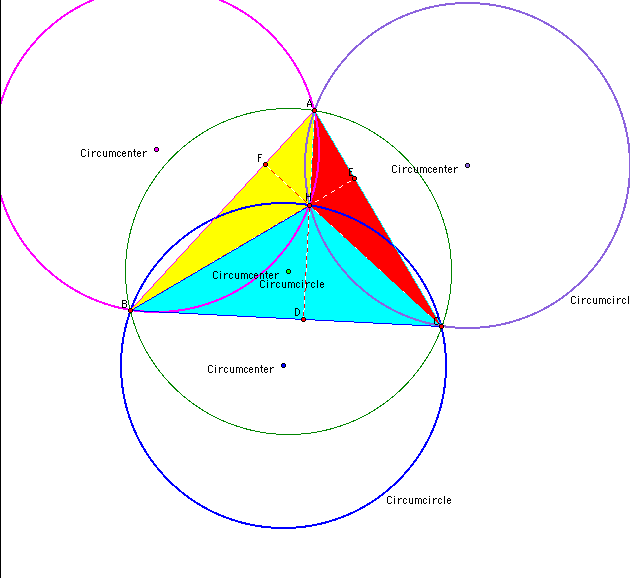
Click HERE to manipulate this sketch in gsp.
Notice that the circumcircles of triangles HAC, HAB, and HBC all go through the orthocenter H. This would be an interesting investigation. Constructing the nine point circle and dialating it would perhaps be key in investigating this conjecture.
I hid three of the circumcircles, so I could investigate the ninepoint circle and the circumcircle for triangle ABC. Here is the construction of the nine point circle and the circumcircle for Triangle ABC:
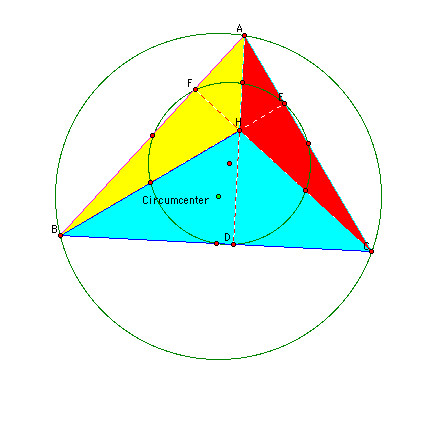
Notice that if I dilate this figure about the orthocenter by a factor of two to one I obtain the following:
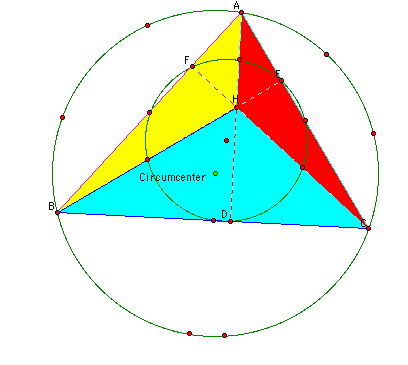
Notice that the dilation is the circumcircle and the nine points of the nine point circle map onto the circumcircle. Now if I do the same thing for triangle HBC, the nine point circle is the same and if the ninepoint circle is dialated around the orthocenter of this triangle I obtain a circle which is mapped onto the circumcircle of this triangle:
This is an interesting investigation and it appears that from this the radii of the four circumcircles are congruent.
It appears that there are lots of interesting relationships here and so I am going to use some of these relationships to prove that:
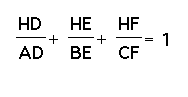
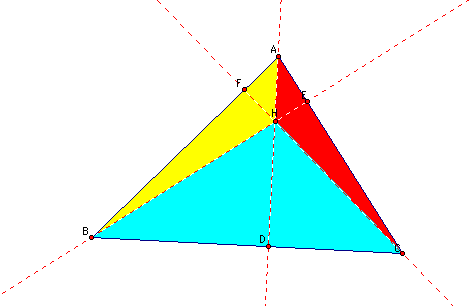
In order to prove this I need to begin by investigating the area of my three triangles:
I know that the formula for the area of a triangle is:
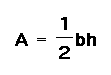
So, the area of triangle ABC is equivalent to:
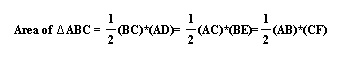
AD, BE, and CF are the altitudes of triangle ABC, so they are the heights of triangle ABC.
Now I also know that the area of the whole triangle ABC is equivalent to the sum of the three smaller triangles inside triangle ABC. In other words:
![]()
Now if I divide by the Area of Triangle ABC I obtain the following:
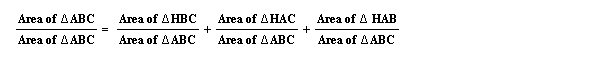
Notice that HD, HE and HF the feet of the perpendiculars, are the altitudes of Triangles HBC, HAC, and HAB. Looking at the ratio I just created I know that are of Triangle ABC over the area of Triangle ABC is equal to one:
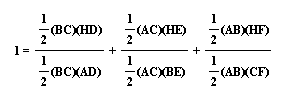
Notice that this is equivalent to:
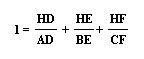
This proves my first conjecture.
I will now set out to prove that:

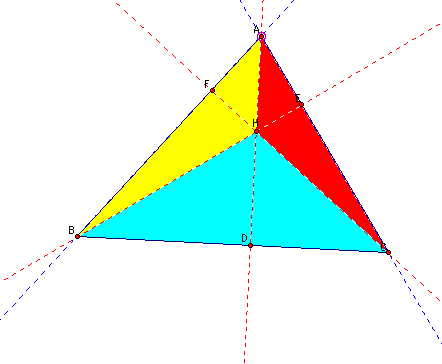
Before I begin, take a look at the triangles again:

Note that :
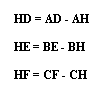
Now if I substitute this into this previous equation:
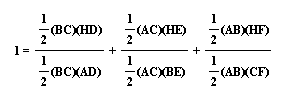
I obtain:
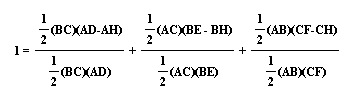
Notice that this simplifies to:
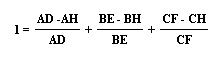
Notice that this is equivalent to:
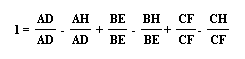
Which is equivalent to:
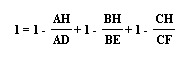
Which equals:
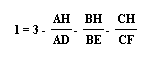
then:
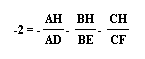
and finally when divided by a negative you obtain:
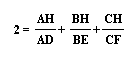
and the proof is completed.
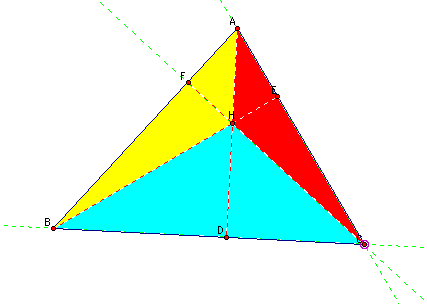
Now what happens if your triangle is obtuse instead of acute? Here is what the construction looks like with obtuse triangle ABC:
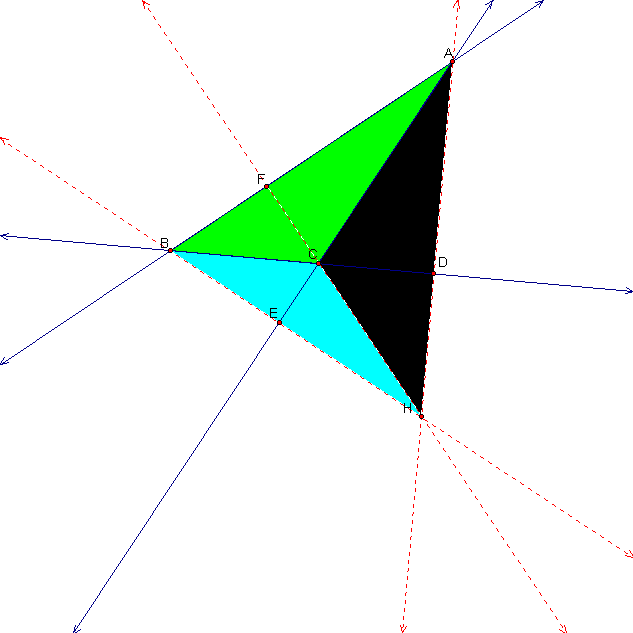
Notice that in this case:
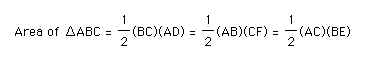
Notice also in this case that:
![]()
Notice that if I divide everything by the area of triangle ABC then:

Notice then by substituting the formulas for the areas of the triangles that:
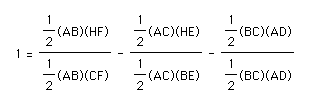
Then:
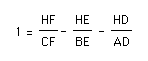
Notice that the first relationship does not hold. When the orthocenter H is moved outside of the triangle then the relationship between the altitudes and the orthocenter of the triangle changes. It stands to reason that if the first equation does not hold the second equation:

will not hold either.
Notice that in this case:
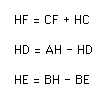
Now substituting that into:
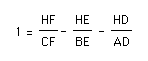
I obtain:
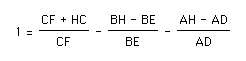
This is equivalent to:
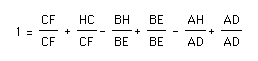
which equals:
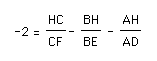
After dividing by a negative I obtain:
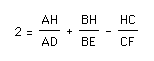
I can see that this relationship does not hold when the orthocenter is moved outside of the triangle either. Therefore, when the orthocenter is moved outside of the triangle the relationship between the orthocenter and the altitudes of the triangle changes.
Author & Contact:
Jennifer Shea