

Problem 1: Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides labeled D,E, and F respectively. Explore (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles and various locations of P. Make a conjecture and prove it.
Problem 2: Show that when P is inside of triangle ABC the ratio of the areas of triangle ABC abd triangle DEF is always greater than or equal to four. When is the area of the ratios equal to four?
Investigation 1:
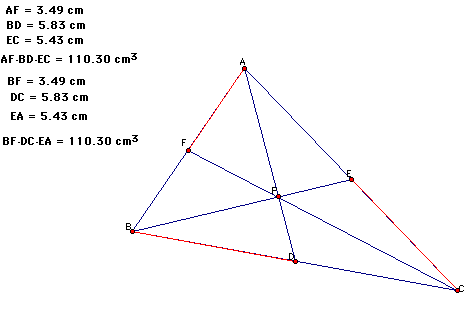
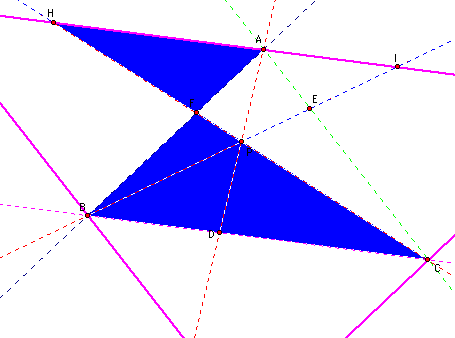
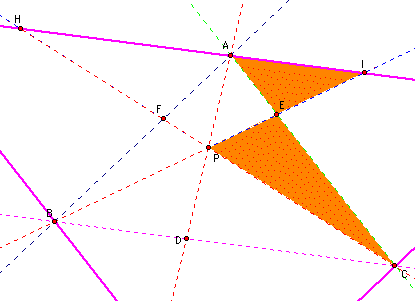
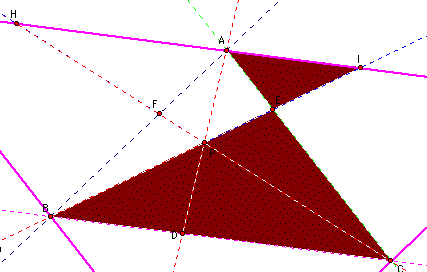
I began my investigation by setting up the construction and choosing point P inside of triangle ABC.
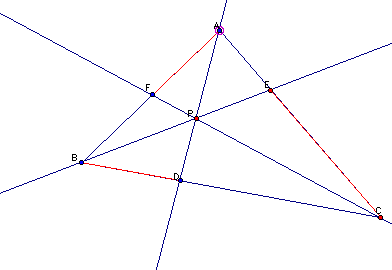
I measured the distances of AF, BD, CE, BF, CD, AE, and then calculated (AF)(BD)(CE) and (BF)(CD)(AE).
I noticed that as I moved my triangle around that (AF)(BD)(CE) and (BF)(CD)(AE) remained the same.
Click HERE to view this sketch so you can investigate what happens as the triangle is moved around.
I can also move the point P around in this sketch and see that (AF)(EC)(BD) = (FB)(AE)(DC).
For this first sketch I chose P as a random point in triangle ABC.
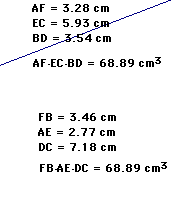
I also investigated what would occur if I chose P to be the orthocenter of my triangle.
If P was chosen as the orthocenter of my triangle (AF)(EC)(BD) was still equivalent to (FB)(AE)(DC).
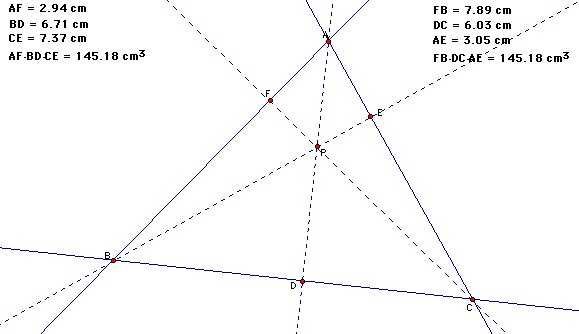
Notice that if I move my orthocenter outside of triangle ABC, that (AF)(BD)(CE) is still equivalent to (FB)(AE)(DC).
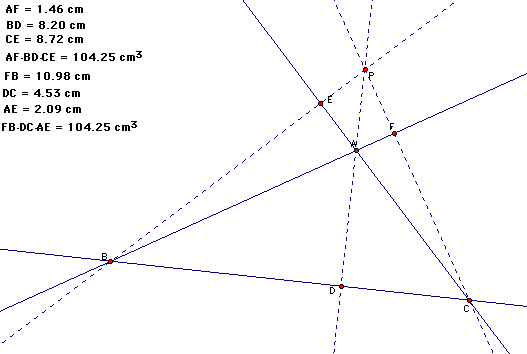
It appears that this observation is generalizable to when P is outside of my given triangle ABC as well.
What if P is the centroid of triangle ABC?
Notice that (AF)(BD)(CE) is still equivalent to (FB)(AE)(DC)
At this point since in moving triangle ABC around and in changing the position of point P, I am ready to make a conjecture.
Since (AF)(BD)(CE) always equals (FB)(AE)(DC) in my observations I conjecture that:
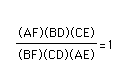
Now that I have a conjecture I am going to try to prove this conjecture.
I know that if I look at similar triangles, that I can form ratios between sides of triangles, so I tried to make parallel lines to form similar triangles.
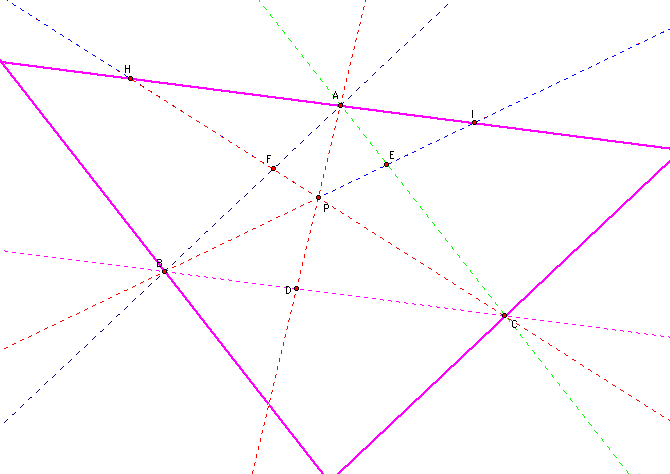
SETUP 1:
One setup of parallel lines I tried was the following:
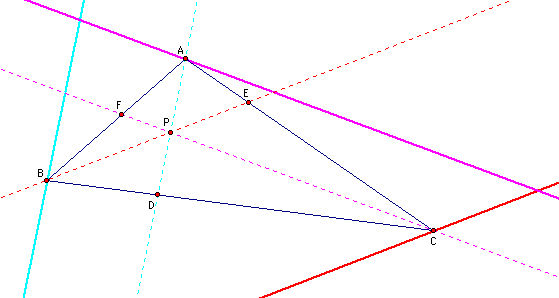
I set the parallel lines up so that pt. A, B, and C would be parallel to a corresponding line through point P.
In this set up I found that triangle BHF and triangle APF were similar.
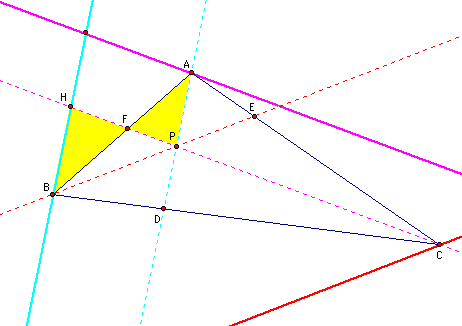
The similarity of these two triangles follows from the AA Similarity Theorem.
<BFG is congruent to <AFP because they are vertical angles
<HBG is congruent to <FAP because they are alternate interior angles.
I know that because these two triangles are similar there sides are proportional.by the definition of similarity.
So, in this case AF/BF = AP/BH = PF/FH
I then thought that it might be possible to show that triangle BPF was similar to triangle EPC since they already have one pair of vertical angles congruent. I also saw several other pairs of triangles that looked like they could possibly be similar however, I ran into some difficulty with finding pairs of alternate interior angles and vertical angles with this setup, so I decided that I should attempt a different setup.
SETUP 2:
This time instead of putting lines parallel from a corresponding line through P to my vertices I instead, tried putting lines parallel to the opposite sides of my triangles through my vertices of my triangle.
Through this setup I found many pairs of similar triangles.
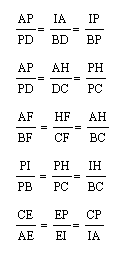
I found the following:

This means that the sides of these two triangles are proportional to one another:
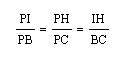
I also found that:

This means that the sides of this triangle are proportional, in other words:
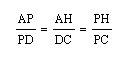
In addition:

This tells us the following:
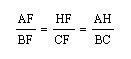
In addition:

This tells us the following:
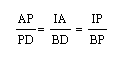
In addition:

This informs us that:
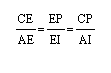
Notice that from these 5 pairs of similar triangles I obtain the following proprotions:
Notice that:
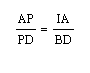
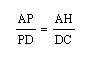
Since this is the case then:
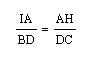
and:
therefore I can say that:
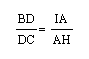
At this point I can say by substitution that:
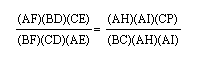
At this point I realized that this does not prove my conjecture, but also that I had overlooked one very important pair of similar triangles:

This gives me the following proportions:
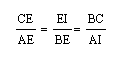
Then, by changing my substitution for :
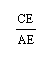
I obtain the following:
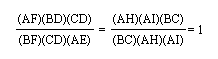
and this is the end of the proof.
This proof is the proof of Ceva's Theorem.
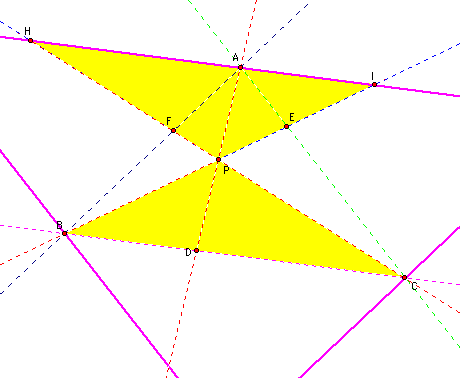
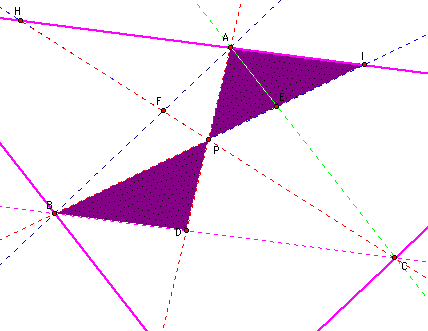
I can also show that when P is inside triangle ABC that the ratio of the areas of triangle ABC and triangle DEF, is always greater than or equal to 4.
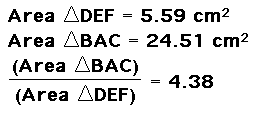
Click HERE to view this sketch and move P around to see that the ratio of the area of triangle ABC to the area of triangle DEF is always greater than or equal to 4.
This ratio is equal to 4, when P is the centroid of triangle ABC. Note that when P is the centroid of triangle ABC that it splits the triangle into four equal areas.
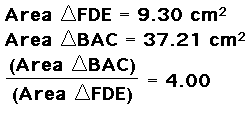
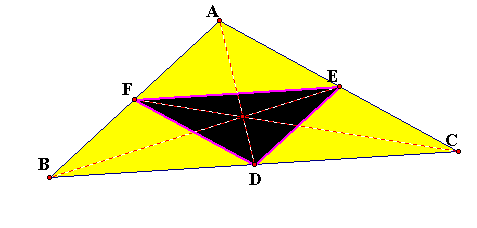
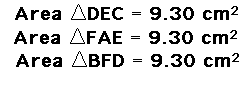
In order to try to prove that the ratio of the area of triangle ABC to triangle DEF was four when P was at the centroid of the triangle I am going to go back to my notion of similar triangles. Because similar triangles give proportional sides in my triangle. Note that when P is at the centorid of triangle ABC, triangle DEF is the medial triangle of triangle ABC.
I know by the Midsegment Theorem that the sides of the medial triangle are parallel to the sides of triangle ABC and also 1/2 their length. A midsegment is simply a segment that connects two midpoints of the sides of a triangle. The sides of triangle DEF are midsegments by nature of the construction of the centroid. Since the three sides of triangle FED are in a 1/2 relationship to the sides of triangle ABC then:
The area of a triangle is (1/2)bh. So looking at these two triangles:
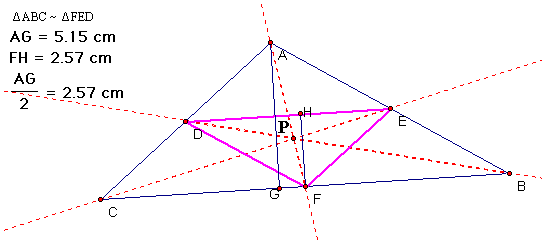
I know that the area of triangle ABC = (1/2)(BC)(AG) and
the area of triangle FED = (1/2)(ED)(FH)
Now, I know that DE is 1/2 the length of BC, and it also appears from measurement that the altitude FH of triangle FED is 1/2 the length of the altitude AG of triangle ABC.
To show that the length of the altitude FH of triangle FED is 1/2 the length of the altitude AG of triangle ABC I return to the idea of similar triangles. I can show that:

These two triangles are similar by the AA Similartity Theorem.
Now I know from the Midsegment Theorem that:
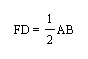
Since this is the case and I have just shown that triangles AGB and FHD are similar I also know that:
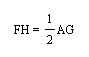
Therefore in looking back at the area of my two triangles:
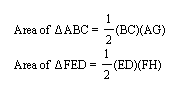
Since I know from the Midsegment Theorem that:
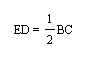
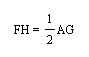
I also know that:
I can say that:
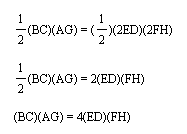
Then:
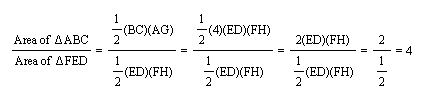
Therefore when P is the centroid of triangle ABC the ratio of the area of triangle ABC to the area of triangle FED is equal to four.
Can I extend this idea to show that when P is inside triangle ABC that the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4?
I think that this idea can be extended by contradiction.
It seems that if I assume that for every P inside triangle ABC that the ratio of the areas of triangle ABC and triangle DEF is always less than four, when P is my the centroid of my triangle ABC I have a counterexample to this statement. Then the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to four.
Author & Contact:
Jennifer Shea