Assignment 12: Volume of
a Box
by
Melissa Silverman
Suppose we begin with a 5x8 sheet of
cardboard. We want to make an open box from this sheet, with the
largest volume possible. How can we construct the box with the
largest volume? To begin, let's draw a picture of what happens
when we create a three dimensional figure from a flat piece of
cardboard.
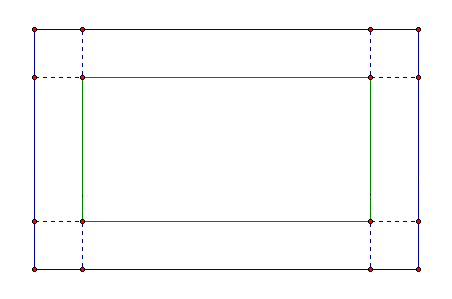By cutting a square piece from each
corner, we get a box whose base is smaller than the original box
(the green rectangle). The width of the base is 5 units minus
two of the squares' lengths. Similarly, the length of the base
is 8 units, minus two of the squares' lengths. The depth of the
box is the same as one side of the square. Thus the dimensions
of the squares cut from each corner determine the depth of the
box.
How big should the squares be in each
corner to achieve the maximum volume of the box? We can use a
spreadsheet to calculate the volume of the box given the dimensions
of the square to be cut from each corner. The length of the base
is 8-2*(Size of Square). The width of the base is 5-2*(Size of
Square). The area of the base is the product of the new length
and width. The volume is the product of the area of the base and
the dimension of the square.
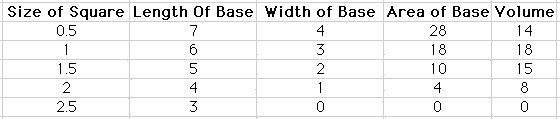
Looking at the chart, we can see that
cutting a 1 unit square from each corner will create a box with
the largest volume. Cutting a square that is larger or smaller
than that results in a smaller. The squares cut from each corner
cannot be greater than 2.5 units. At that point, the width of
the base would be 0 units, and a box would not be formed. If the
squares cut from each corner are small, the area of the base is
large, but the height of the box is small, resulting in a smaller
volume.
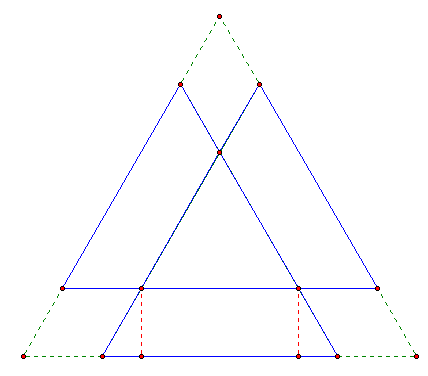
What if we began with an equilateral
triangle, with side lengths of 10 units? We could construct a
triangular box by cutting a rhombus from each corner. We will
leave tabs on each of the three side pieces (see the red dashed
lines in the picture below). How could we cut the triangle so
that we get a triangular box with the largest volume?
We can use a spreadsheet to calculate
the volume of the box given the dimensions of the rhombus. CLICK HERE to open the spreadsheet
on your own computer.
We begin with the height of the rhombus.
Then we can use the properties of a 30-60-90 triangle to figure
out the length of the tab. The length of the new base is one rhombus
length and one tab length shorter on each side. Subtracting two
rhombus lengths and two base lengths from the triangle's base
of 10 units yields the length of the new base. To figure out the
height of the new triangle, use the Pythagorean theorem. Subtract
the square of half the base length from the square of the base
length. The square root of that value is the base height. The
area of the box base is the product of one half, the base height,
and the base length. The volume of the box is the product of the
area of the base and the height of the rhombus.
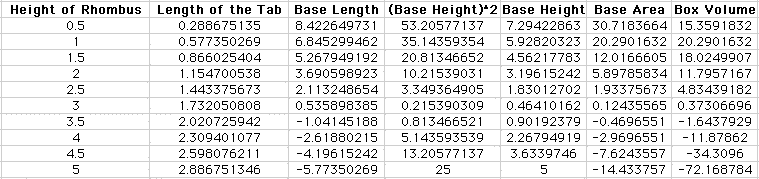
We can see from the chart that the
rhombus that will give us the largest volume is a rhombus whose
height is 1 unit, just like the rectangular box that was also
maximized with a square of 1 unit cut from each corner.
This problem is often seen in calculus
curriculum as a min/max problem using derivatives. Using a simple
diagram and a spreadsheet, middle school students could develop
the same ideas using their math background. This problem is important
in middle school curriculum for several reasons.
First of all, it is a great way to
use both area and volume in one problem. Having students combine
the concepts of 2 dimensional area and 3 dimensional volume is
a great exercise. The students must practice visualizing both
area and volume. Making a 2 dimensional pattern for a three dimensional
figure is often in the middle school curriculum. Secondly, this
problem does involve some simple algebra, with the dimension of
the square as one of the variables. This is a great application
of algebra in that it connects geometry and algebra. Lastly, this
problem develops the ideas they will need in higher level mathematics,
such as algebra and calculus.
I also like the potential for exploration
built into this problem. Students may ask about many things. What
would happen if we started with a square sheet instead of a retangular
one? What if we tried the same procedure with a triangular piece?
Or any polygon? Why do we have to cut a square out of the corner?
Asking students to use both computer technology and actual construction
with paper to test their ideas could lead to some really great
mathematical discovery.
Assignment
11 | Home Page | Assignment
1