Assignment 7: Tangent Circles
by
Melissa Silverman
Consider two circles, with one inside
the other. How could you construct a circle tangent to both circles?
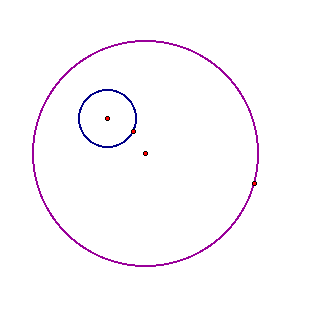
Begin by constructing a line through
the center of the larger circle. Then construct a congruent circle
(to the circle already inside the circle) whose center is where
the line and the larger circle meet.
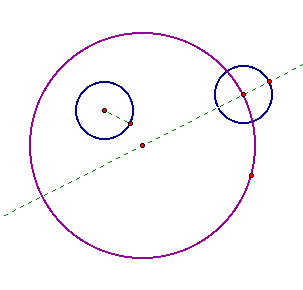
To find a circle tangent to the large
purple circle and the blue circle inside of it, we need to construct
a circle whose diameter is the length of the blue inscribed circle
to the purple circle. From that we can conclude that the radius
of this circle is half of that distance. Constructing a segment
between the two blue circles and bisecting it will provide the
base of the equilateral triangle we are looking for.
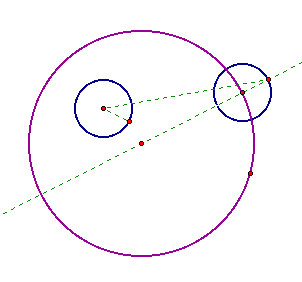
If we bisect this segment and mark
the point of intersect between the perpendicular of this segment
and our original green dashed line, we have the equilateral triangle
that we need to construct a circle tangent to the purple and blue
circles.
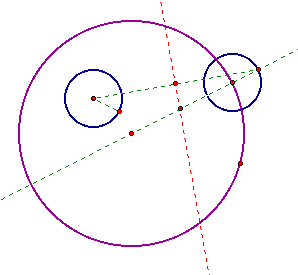
The point where the red and green dashed
lines intersect is the center of a circle that is tangent to both
the blue and purple circle.
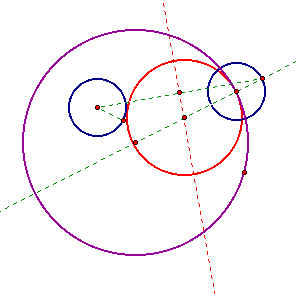
The red circle is tangent to the inner
blue circle and the purple circle. The red tangent circle can
be moved around to illustrate many possible tangent circles. To
use the tool and manipulate the construction yourself, CLICK HERE. In the pictures below,
notice how the size and location of the red tangent circle differs,
but the original two circles do not change.
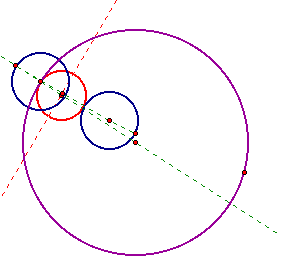
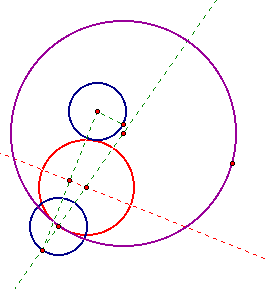
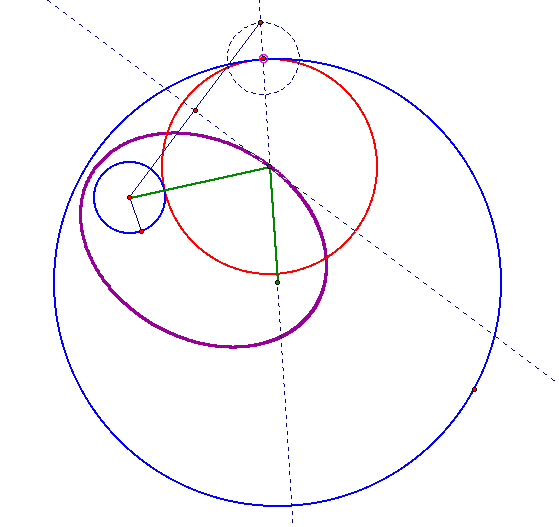
Tracing
the center of the tangent circle (red circle) creates an ellipse
(the purple ellipse below). The two green segments represent the
two lengths whose sum never changes as the center of the red circle
moves around the ellipse. One green segment is the radius of the
red circle. The other is the sum of the radii of the red circle
and the solid blue circle.
In a middle school classroom, I think
this construction would be hard for the students to understand
conceptually. The notion of using an equilateral triangle to construct
the tangent circle might leave the students confused. The construction
is simple enough where students could follow a set of steps, but
the reasoning behind the steps would most likely be lost.
As a teacher, I think that making the
construction yourself and showing it to your students as an instructional
tool would have many benefits. Students could sketch what they
think the tangent circle to the two circles would look like on
their own papers and compare their sketches to the GSP construction.
By moving the tangent circle around, students can see that there
are infinitely many ways to draw a circle tangent to the two circles.
Animating the construction can be motivating and exciting for
the students. Animating it after they have thought about and predicted
the outcome would be a neat presentation.
In a high school classroom, this would
be great for illustrating ellipses. This is a great demonstration
of the definition of an ellipse. Animating the construction to
form an ellipse helps students visualize exactly where an ellipse
comes from. This is a far better method than just having students
memorize the formula of an ellipse from the textbook and forcing
them to accept why the formula is written the way it is and what
the parts of the formula mean.
Assignment
6 | Home Page | Assignment
8








