Assignment 9: The Pedal Triangle
by
Melissa Silverman
To construct a pedal triangle, begin
with a triangle (whose sides are lines, not line segments). Pick
any point on the plane, Point P. Construct perpendicular lines
from the sides of the triangle to Point P. Mark the intersections
of those perpendicular lines and the sides of the triangle. Those
three points of intersection connect to form the pedal triangle.
In the construction below, the pedal triangle is drawn in red.
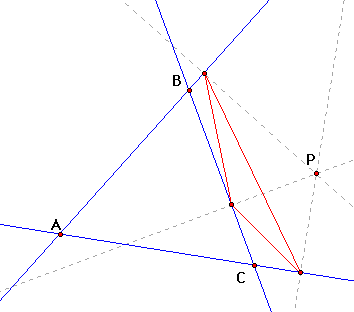
Using GSP to make a pedal triangle
allows one to move Point P on the plane and observe how the position
of Point P affects the pedal triangle. For example, what happens
if Point P is merged with the centroid?
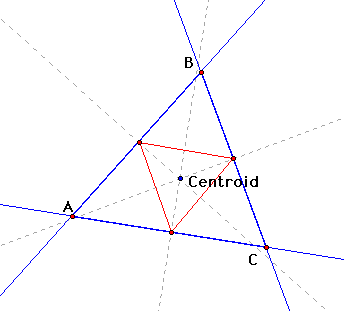The pedal triangle becomes the medial
triangle when Point P is merged with the centroid. The pedal (or
medial) triangle divides the triangle in to 4 congruent triangles
that are similar to Triangle ABC.
We can also investigate what happens
when Point P merges with the orthocenter or circumcenter?
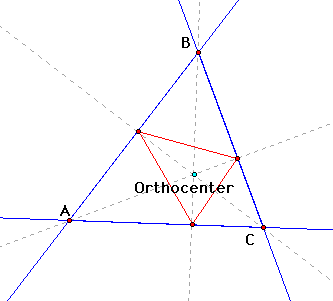The pedal triangle is inside Triangle
ABC, cutting it into 4 triangular parts. The parts are neither
congruent to each other nor similiar to Triangle ABC.
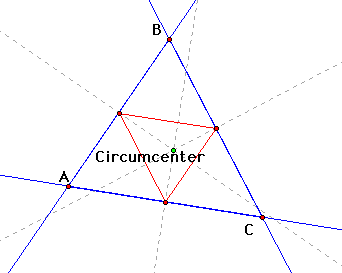When Point P is merged with the circumcenter,
the pedal triangle is again inside Triangle ABC, cutting into
4 triangular parts. The parts are not congruent.
If Point P is on the circumcircle,
the pedal triangle morphs into a straight line. Similarly, if
Point P is on one of the vertices of Triangle ABC, the pedal triangle
is a straight line because the vertices are a part of the circumcircle.
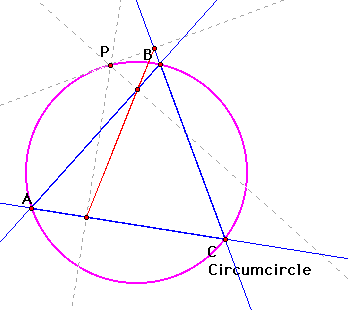Above, notice that when Point P is
on the circumcircle, the pedal triangle becomes a straight line.
Similarly, when Point P is on a vertex, the pedal triangle is
a straight line because the vertex is part of the circumcircle.
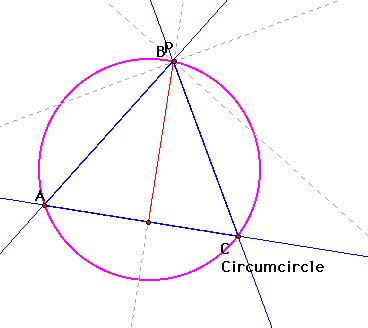
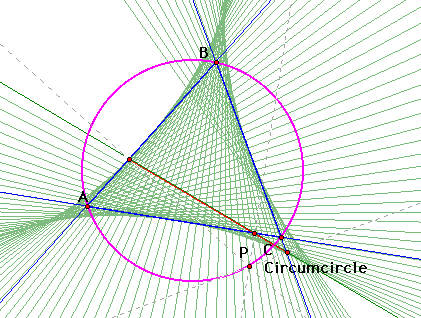
If you trace the pedal triangle line
as Point P is moved along the circumcircle, the result is the
envelope of the Simson line.
Assignment
8 | Home Page | Assignment
10