NINE POINT CIRCLE
BY
Audrey V.
Simmons
What is the nine-point circle and how is it created?
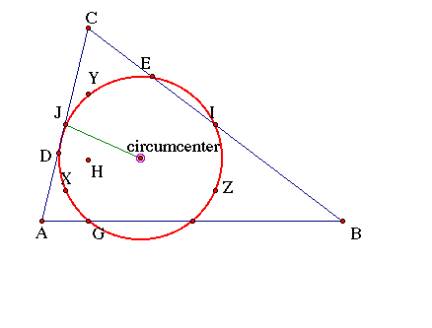
The nine-point circle is a circle comprised of the three feet of the altitudes of a triangle, the three mid-points of the segments from the orthocenter to each respective vertex, and the three mid-points of the sides. Let’s construct the circle in stages.
Step 1
Draw a triangle. Find the midpoints of each side. If we connect these midpoints, they would form a medial triangle.
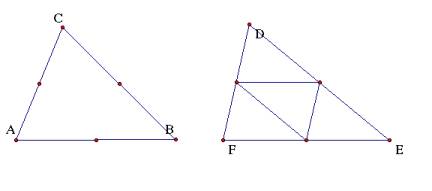
Midpoints shown Medial Triangle
Step 2
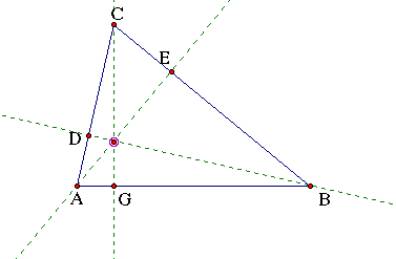
Using the original triangle we will construct three perpendicular lines. One line will be drawn from each vertex to the opposite side.
Segment AE is perpendicular to segment BC
Segment BD is perpendicular to segment AC
Segment CG is perpendicular to segment AB
The point where the three altitudes meet is called the orthocenter (H).
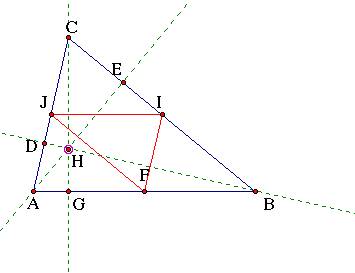
Put all points together on the same graph and it should look like the construction below. The red triangle is the medial triangle. We now have six points for our nine point circle (J,D,G,F,I,E).
Step 3
Find the midpoints of each of the segments CH, AH, BH. They are labeled X, Y, Z. They will be the last three points on the nine-point circle.
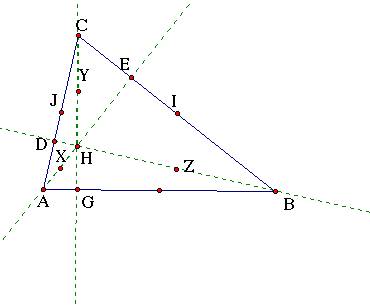
Step 4
Find the circumcenter of the medial triangle. You can find the circumcenter by finding the midpoint of each side. Then find the perpendicular to each side at its respective midpoint. It is the center of the nine-point circle. You can also use the circumcenter of the orthic triangle. You can not use the circumcenter of the original triangle.
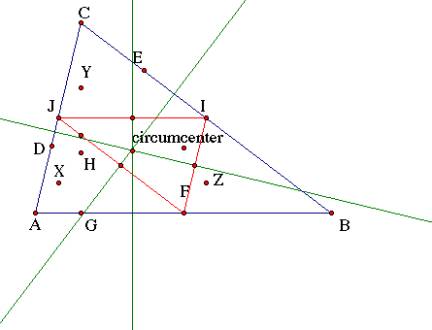
The distance from the circumcenter to point J or I or F is the radius of the circle. This circle is also the circumcircle for the medial triangle.