
Pedal Triangles
By
Audrey V. Simmons
In this assignment we will be looking at the Pedal triangle and some of its unique characteristics. Let’s first look at the construction of the pedal triangle.
Step 1: Construct a triangle
Step 2: Pick an arbitrary point in the same plane. The point can be inside or outside the triangle. Identify the point (P in this case)
Step 3: Draw a perpendicular from point P to each side of the triangle. The sides of the triangle may need to be extended so the perpendiculars have a point of contact.
Step 4: Connect the 3 points of intersection to form the pedal triangle.
Use the script tool of the pedal triangle to see what happens when the arbitrary point is located in different places in relation to the triangle.
Click here.
If the pedal point can be located anywhere on the plane of the triangle is there any significance when the pedal point is the centroid, the incenter or the orthocenter? Let’s look at these possibilities.
Pedal point and the centroid are concurrent.
Click HERE to see the configuration.
Some discoveries may include:
v Even though the centroid always stays inside the triangle the pedal triangle does not.
v There appears to be no common area relationships between the original triangle, the pedal triangle, or any of the internal triangles. Even though the areas in the original triangle ABC formed by using the centroid as a vertex are congruent. Using the same centroid, the one that is concurrent with the pedal point does not give three congruent triangles.
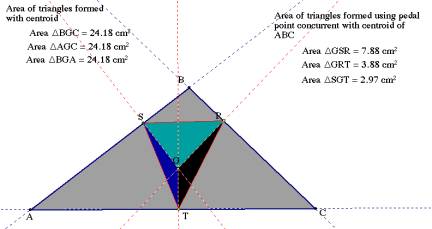
v The original triangle and the pedal triangle do not have concurrent incenters or orthocenters.
v The Euler lines of the two triangles do not intersect in any special way, ie. perpendicular.
v If one tested the ratio of the segments into which the construction of the pedal triangle divides the sides of the triangle, it would not be a golden ratio.
Pedal point and the incenter are concurrent.
Click HERE to experiment with the configuration.
Some discoveries are:
v Even though the orginal triangle can be a right triangle, the pedal triangle approaches a line as the angle approaches 90 degrees.
v The pedal triangle always remains inside of the original triangle.
v The ratio of the measure of the area of the pedal triangle to the area of the remaining remnant of the original triangle is not constant.
v The incircle of triangle ABC is the circumcircle of the pedal triangle.
Click here to see how it is always true.
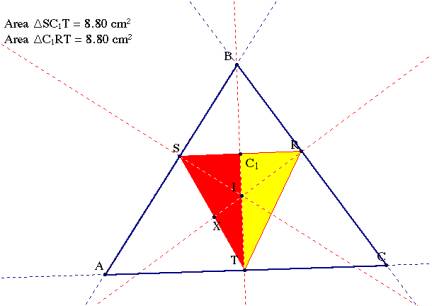
v When the incenter lies on any of the angle bisector from one of the verticies of the original triangle to the midpoint of the opposite side, the area of the pedal triangle is bisected. See below for one example.
Pedal point and the orthocenter are concurrent
Click HERE to see what you can discover.
Some discoveries are:
v The pedal triangle does not stay within the boundaries of triangle ABC.
v There does not seem to be any common ratio between the area of the pedal triangle and the area of the original triangle.
v (As there is a 1:4 ratio with the medial triangle its original triangle.) Click here to compare areas.
v The ninepoint circle is the circumcircle of the pedal triangle.
Click here to see what happens as the orthocenter (pedal point) is moved around.
There are many other explorations that can be done with the pedal triangle that are not covered in this assignment. Try some on your own.