The Department of Mathematics Education

J. Wilson, EMAT 6680

EMAT 6680 Assignment 3

Last modified on August 18, 2002.

The attached 4-page paper is the start of an article that might appear in a journal such as the Mathematics Teacher -- the audience being mathematics teachers who might use some of the ideas for instruction.

It is a start; incomplete, unclear, maybe in error; maybe glossing over significant points and stressing some obvious or trivial points.

Your assignment:

Sign on as a co-author. Rewrite and complete the article. This means you must come to grips with whatever points are to be essential, what to add, what to delete, and what to edit. The "different" approaches to this topic are really in the graphs in the xb, xc, or xa planes. You might want to examine a bunch of these before trying to re-write.

Some Different Ways to Examine

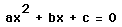
by

James W. Wilson and Matthew J. Tanner
University of Georgia

It has now become a rather standard exercise, with available technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant. From these graphs, discussion of the patterns for the roots of

can be followed. For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

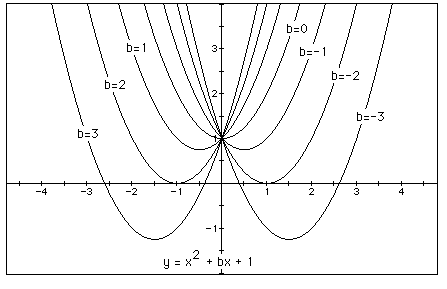
We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis (the point (0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b = 2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersects the x-axis twice to show two negative real roots for each b.

Now consider the locus of the vertices of the set of parabolas graphed from

.

Show that the locus is the parabola

The vertex of a parabola is defined as the ordered pair (x,y) for which the named parabola reaches its global maximum or minimum.  In this case, the global maxima are reached at the values of x for which the value of first order derivative is 0, that is, the value of x where 2x + b = 0  for a given value b.  By inspection, the function reaches its global minima at values

.

at the ordered pair

.

Since the graph of the locus interpolates these ordered pairs, we may say that for any rational number  b

and

.

 

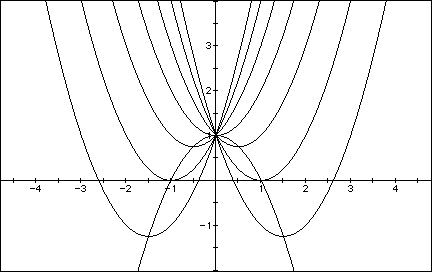
Graphs in the xb plane.


Consider again the equation

Now graph this relation in the xb plane. We get the following graph.

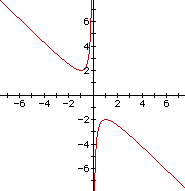
If we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.

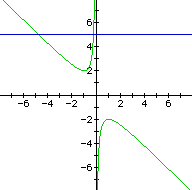
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.

Consider the case when c = - 1 rather than + 1.

 

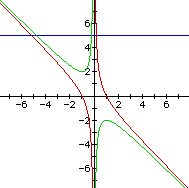
Reciprocity of Roots

 

We know that in the case where c = +1 that the graph depicts all values of  x  and  b  such that

,

These observations immediately follow:

 

1.      The function is undefined at  x = 0 and has a corresponding vertical asymptote.

2.      The function has two extrema, one in quadrant II and one in quadrant IV where the first order derivative

,

that is, 1 and –1 respectively.

 

3.      The value of the function at its extreme is 2 and –2 respectively.  The absolute value of the function cannot assume a value less than 2.

 

4.      There is a one-to-one correspondence between values of  x  greater or equal to 1 and its reciprocal value less than or equal to 1 which will satisfy the equation for any value of  b  of absolute value greater to or equal to 2. 

 

In contrast, when  c=-1, notice that the function has no extrema.  While the equation

remains undefined at zero and so has a corresponding vertical asymptote, the first order derivative test for extrema

has no real solutions.  In further contrast, if it is true for any value  x  that

,

then it is not possible for it to be true for its like-signed reciprocal with the trivial exception of 1 and -1 since

.

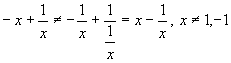Instead, there is a one-to-one correspondence between all (without exception) values of  x  and the opposing sign reciprocal. 

.

 

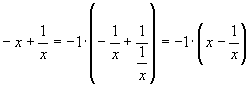Uniqueness of Roots

 

For the equation

to have real roots, there must be a factorization

with  n1  and  n2  such that

.

The intersection of the graph of   b=5  with the graph of the equation  and  shows there to be, at most two roots for any value of  b.  It can be shown that these roots are unique by the following  proof.  Suppose n1  and  n2  are numbers such that .  Next suppose there also exist two numbers m1  and  m2 each distinct from n1  and  n2 such that .

,

so,

.

Since

 

Factoring

.

So

.

This is a contradiction which established the uniqueness of n1  and  n2 as the graph suggest.

 

 

Graphs in the xc plane.In the following example the equation

is considered. If the equation is graphed in the xc plane, it is easy to see that the curve will be a parabola. For each value of c considered, its graph will be a line crossing the parabola in 0, 1, or 2 points -- the intersections being at the roots of the orignal equation at that value of c. In the graph, the graph of c = 1 is shown. The equation

will have two negative roots -- approximately -0.2 and -4.8.

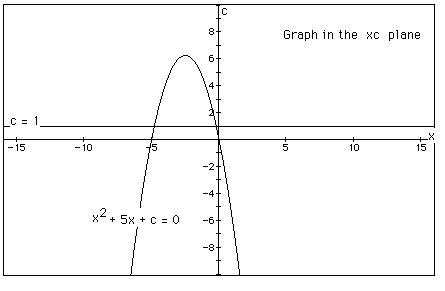
There is one value of c where the equation will have only 1 real root -- at c = 6.25. For c > 6.25 the equation will have no real roots and for c < 6.25 the equation will have two roots, both negative for 0 < c < 6.25, one negative and one 0 when c = 0 and one negative and one positive when c < 0.  This can be seen as a necessary consequence of the quadratic formula.  Each root must satisfy

which only has real solutions for  . 

Send e-mail to jwilson@coe.uga.edu

Return to EMAT 6680 Home Page