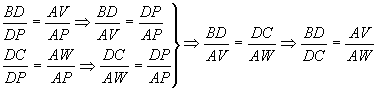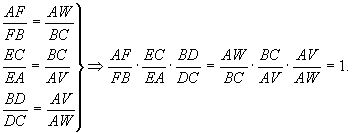Department of Mathematics Education

J. Wilson, EMAT 6680

---

EMAT 6680

Final Assignment

Matthew Tanner

EMAT 6680

Final Assignment

July 26, 2004

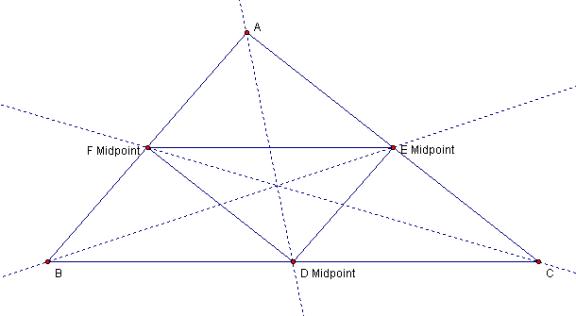
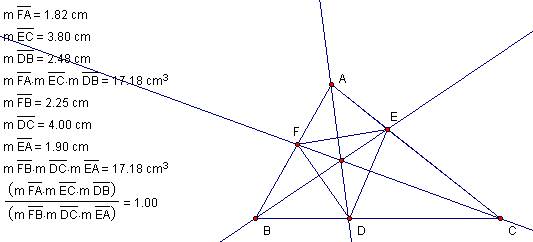
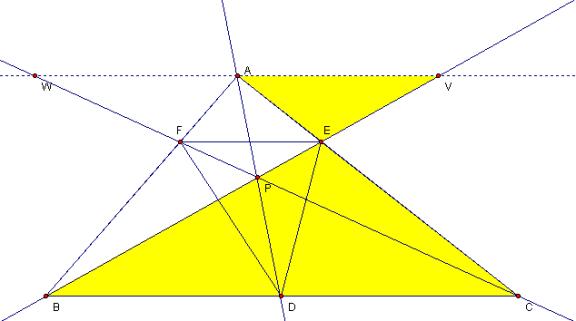
A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

The ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is one for a number of configurations of shape and locations of P.

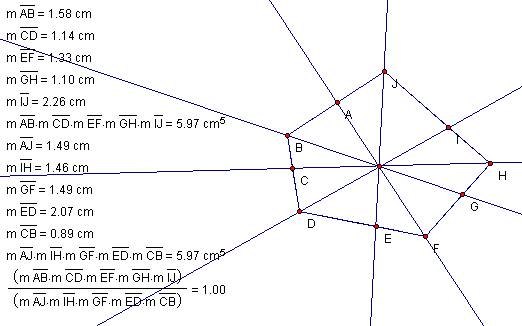
The same is true for polygons of five sides – maybe for all polygons with an odd number of sides.

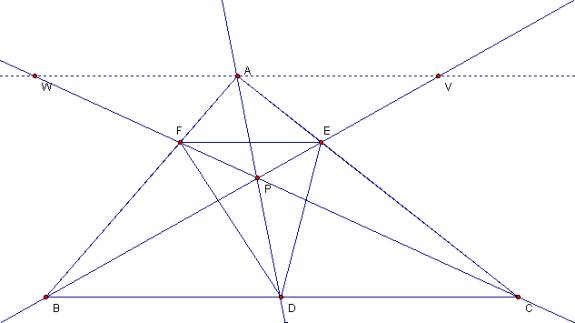
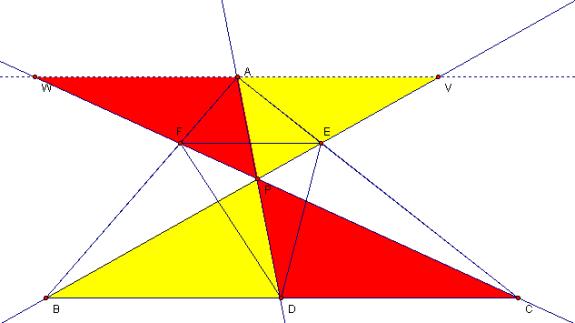
B. Conjecture? Prove it! (you may need draw some parallel lines to produce some similar triangles). Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Show a working GSP sketch.

There exists a fundamental relationship of ratios of the segments of sides of a triangle divided by lines emanating from the opposite vertices and passing through a common central point.

Introducing a line through a vertex parallel to the opposite side produces useful congruencies.

Since segments WC and AB cross parallel lines

and since are opposite angles, they are congruent.

So triangles AFW and BFC are congruent and

(1) .

Similarly triangles AEV and BEC are congruent

so

(2) .

Next, observe that triangles WAP and CDP are congruent and triangles VAP and BDP are congruent.

From this we can derive

(3) .

From (1), (2), and (3) we derive

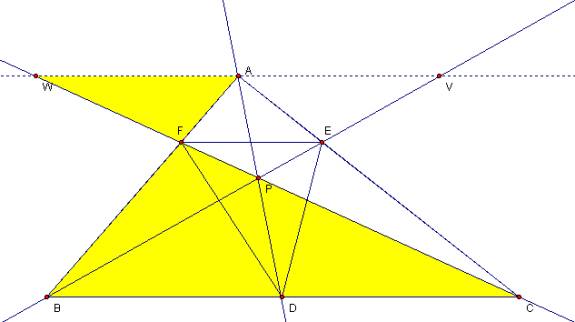
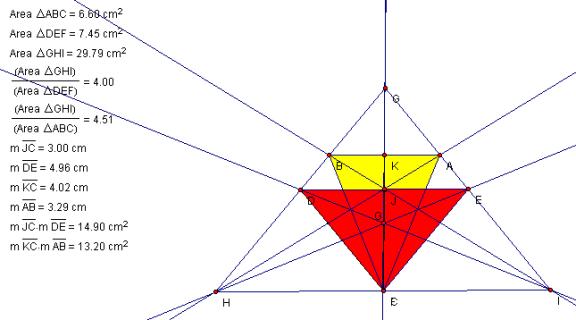
C. Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?.

I assert that the ratio of triangle ABC to triangle DEF is exactly four when the vertices of triangle DEF are located at the midpoints of the sides of triangle ABC – that is, when the junction is located at the centroid. Notice that points E and F each inherit half the horizontal components of segments AB and AC respectively – each in opposing directions, so segment EF is half the length of BC. Similarly segment ED is half that of AB and DF half that of AC. So ED = AF = BF, BD = CD = EF, and DF = CE = AE. So triangles AEF, BDF, CDE, and DEF are all equivalent so the ratio of triangle ABC to DEF is exactly 4.

Perhaps anecdotally, we see that when moving the center of the inscribed triangle away from the centroid, an amount is added to the altitude of the triangle while the base is lessoned by a scalar multiple resulting in a smaller area and a higher ratio in comparison to the principle triangle – at least intimating that the minimum ratio of the principle triangle to the inscribed triangle is 4.