Department of Mathematics Education

J. Wilson, EMAT 6680

Matthew Tanner

EMAT 6680

Write-up #1

June 24, 2003

SELECT ONE PROBLEM TO WRITE UP AND POST TO YOUR WEB PAGE AS HOMEWORK.

3. Find two linear functions f(x) and g(x) such that their product

h(x) = f(x).g(x)

is tangent to each of f(x) and g(x) at two distinct points. Discuss and illustrate the method and the results.

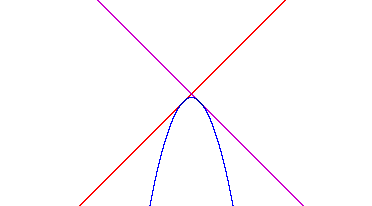
First observe that, because f(x) and g(x) are linear functions, they are of the form

.

Next, suppose the two functions are symmetric about the Y-axis. They’re my lines. And besides, I posit without proof that we can accomplish this by linear transformation. This has the effect that a₁ = -a₂ and b₁ = b₂. So

and

.

Note that, since g(x) and f(x) must each be tangent to h(x) and the derivative of a function is equivalent to its slope, the values of x for which f(x) and g(x) are tangent to h(x) must respectively satisfy

for f(x)

for g(x).

By inspection, the values and satisfy the equations. Arbitrarily selecting a = 1 gives the values .

Precisely because h(x) is the product of f(x) and g(x), the points where f(x) and g(x) are tangent are also their respective zero points. So

,

.

Note that since the tangent points and hence the zero points are inversely associated with the slopes of their respective functions, any value for a may be chosen. Click here for the demo.