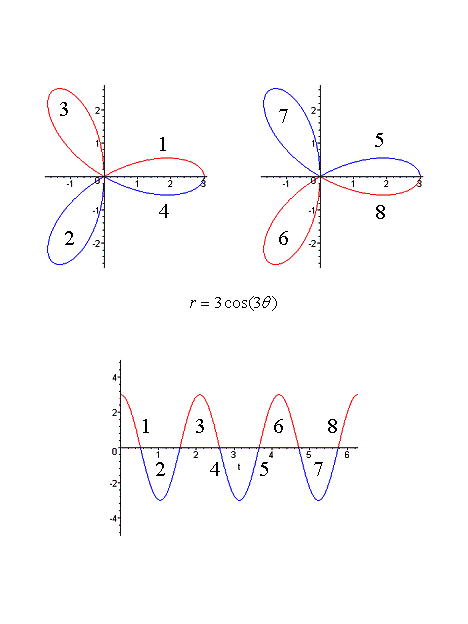Department of Mathematics Education

J. Wilson, EMAT 6680

Matthew Tanner

EMAT 6680

Write-up #11

July 16, 2004

Like the Cartesian coordinate system, polar coordinates offer another unique description of the location of a point in space. Whereas points referred to using a Cartesian coordinate system refer to an original point and n vectors meted parallel to axes called bases, points referred to using a polar coordinate system refer to a distance from an original point according to a deflection from n-1 reference vectors. Sets of points described simply using a Cartesian system are frequently cumbersome and protracted using a polar system and vice versa.

In this study, simple polar equations of the form

r = a + b cos(kӨ)

are investigated.

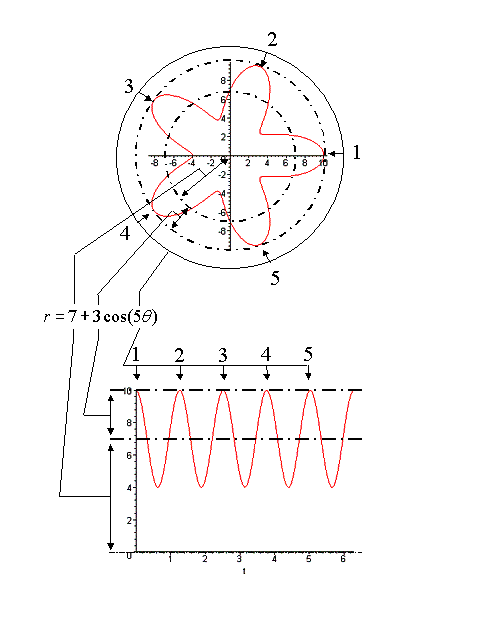
Figure 1

Referring to a Cartesian analogy of the graph of a polar equation, we see that within the range of 2p, the graph completes 5 cycles because of the scalar multiple of q. The difference between the maxima and the mean of the graph (1 for the cosine function without a scalar) is 3. The mean amplitude of the graph (0 for the cosine function) is 7.

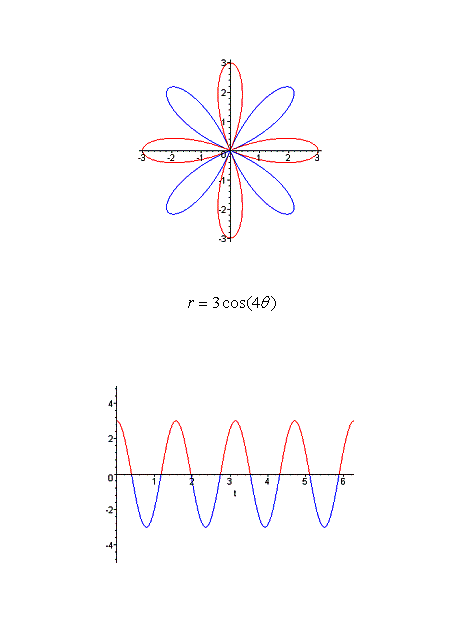
Figure 2

Polar graphs of equations of the form r = b cos(kq) do not have a shift in the mean amplitude of the cosine function. We observe that when k is an even integer, the number of “petals” is double – half correlating with the positive semi-cycles of the Cartesian graph of the cosine function and half correlating with the negative semi-cycles.

Figure 3

When k is an odd integer, we note that the number of petals is not doubled. This is due to the graph of the function between 0 and p coinciding with the graph of the function between p and 2p.