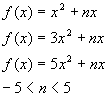![]()
Department
ofMathematicsEducation
J. Wilson, EMAT 6680
Matthew Tanner
EMAT 6680
Write-up #2
June 27, 2003
A quadratic function is given the general form.
f(x)=ax2
+ bx + c.
Varying each of the constants a, b, and c, while holding the remaining two constant illustrates their effect on the value of the function.
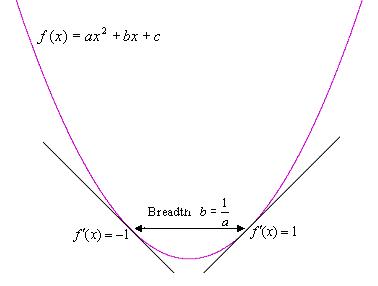
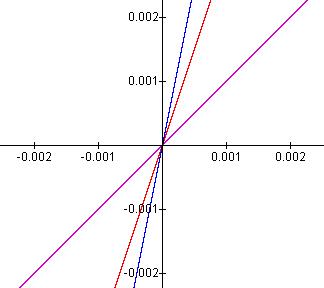
Varying the coefficient a has the effect of varying the breadth of the graph of the function. Let p1 and p2 be the values of x where the slope of the function is 1 and 1 respectively. That is, f(p1)=-1 and f(p2)=1. These are two arbitrarily chosen but easily recognizable landmarks on any graph of a quadratic function.
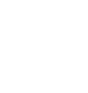
![]()
Since
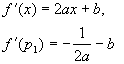
and
![]() .
.
The distance between p1 and p2 is
![]() .
.
This can further be demonstrated by observing that since the second derivative the quadratic function is everywhere
![]()
the breath is
![]() .
.
It is clear that the breadth of the graph of a quadratic as defined above is characterized by a alone. The effect of the coefficient b is small when x is large.
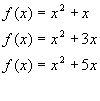
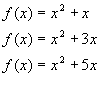
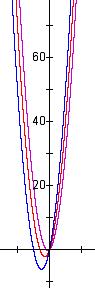
However, proximal to the Y-axis, b plays a larger role. The coefficient b describes the slope of the quadratic function at the Y-axis.
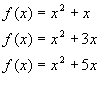
Because the coefficient b does not affect the breadth of the graph but does dictate the slope at the Y-axis intersection, taken together, the effect can be seen as constraining the graph to shift along a parabolic path.
Clickhe graph above for the demo
The c-coordinate has the simple effect of shifting the graph of the function along the Y-axis.
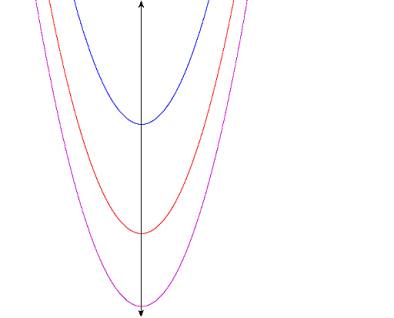
It is interesting to note the effect laterally shifting the graph of the function hason the c -coordinate. Consider the graph of the function
![]() .
.
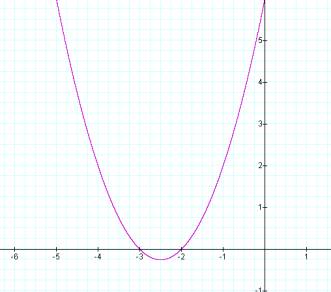
![]()
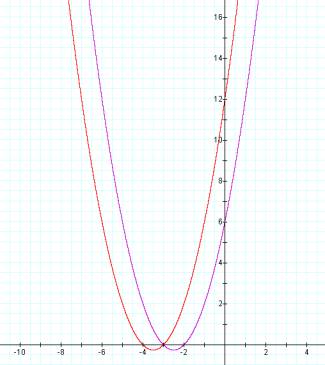
The function has real roots at3 and -2 as can be seen in the factorization f(x) = (x+3)(x+2). The slope of the function at x=0 is 5 as the b-coefficient indicates and the Y-intercept is 6 . Now additionally consider the function
![]()
![]()
![]()
The new function has the same breath
(second derivative) as the original function and real roots at 4 and 3 so the
effect has been to shift the graph of the original function to the left. Also note that the new function has a slope
of 7 at the Y-axis and Y-intercept of 12.
The difference in c-coefficients corresponds to the difference of
the Y-intercept of the original function and the value of the original function
evaluated for the value of the first derivative corresponding to the slope at
the Y-axis of the new function. It is evident
that the lateral transformation can be thought of as a composition of the
transformation brought about by a change in the b-coefficient and the
vertical transformation brought about by a change in the c-coefficient.