

![]()
Department
ofMathematicsEducation
J. Wilson, EMAT 6680
Matthew Tanner
EMAT 6680
Write-up #4
June 24, 2003
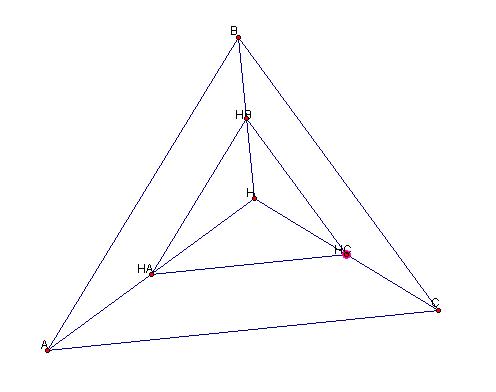
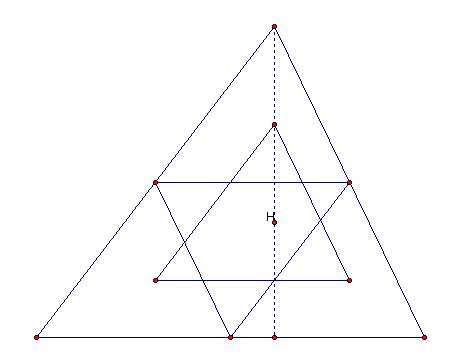
Take an acute triangle ABC. Construct the orthocenter of ABC and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.
Lemma: First observe that the line segment defined by the midpoints of any two sides of a triangle is parallel to the remaining side.
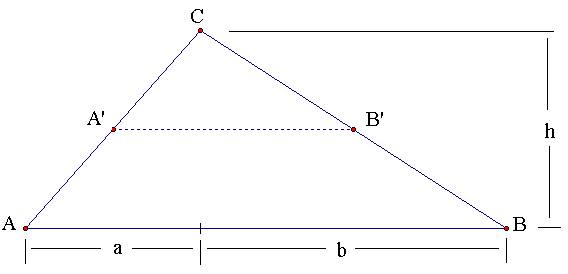
This can be demonstrated by noting that the vertex C of the two sides is
Tangentially and in general, a midpoint on a line is the midpoint of all its components in every linearly independent basis.
Since the segments derived from the midpoints of the lines connecting the points on the original triangle to the orthocenter are all respectively parallel to their corresponding side of the original triangle, the triangle formed by these segments is similar to the original triangle. This can be proved by showing that, since for instance, AB and HAHB are parallel, angles HHAHB and HAB are equivalent. Similarly, since AC and HAHC are parallel, HHAHC and HAC are equivalent. So HBHAHC and BAC are equivalent. The remaining angles can likewise be shown to be equivalent to show that the inner triangle HAHBHC is similar to ABC.
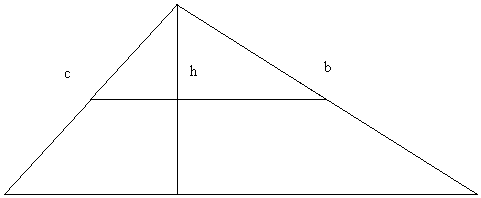
A similar proof may be constructed by noting from above that the segment defined by the midpoints of any two sides of a triangle is half the length of the remaining side. Since the segments form by the midpoints are all half the length of the corresponding side of the original triangle, the triangle formed by these segments in similar to the original. Additionally, observe that since all segments are half the length of the corresponding side of the original triangle, and since the altitude may be derived from the length of the sides, the area of the triangle formed by the segments is ¼ that of the original triangle.
a/d a
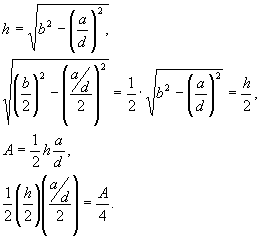
Observe the relationship between the triangle formed by the segments defined by the midpoints of the sides of the parent triangle and medial triangle.
Since each of the sides of the medial triangle are defined by the midpoints of two of the sides of the parent triangle, its length is half that of the remaining side, as we have seen. Since each of the sides of the medial triangle is half that of the corresponding parent side, it is similar to the parent.
An alternating proof may be constructed by observing that for each of the angles of the parent triangle, the corresponding angle of the medial triangle located at the midpoint of the opposite side of the parent represents the complementary angle implicit in opposing vertices of a parallelogram. Since each of the angles of the medial triangle is complementary to one of the parent triangle, they are similar.
In contrast to the triangle formed by the segments defined by the midpoints of the sides of the parent triangle which has sides corresponding to adjacent sides of the parent, since the medial triangle has sides defined by points bisecting the sides adjacent to the corresponding parent sides, the medial triangle is symmetrically inverted with regard to the parent triangle and the triangle formed by the segments defined by the midpoints of the sides of the parent. Note that since the triangle formed by the segments defined by the midpoints of the sides of the parent and the medial triangle both have sides half the length of a corresponding parent side, they are congruent to each other.
The Euler’s Line corresponding to the parent and child triangle are likewise congruent and collinear. Notice first that since the child triangle is defined by the midpoints of the line segments defining the parent orthocenter and since the extension of these segments both intersect a vertex of the child triangle as well as from a 90° at the intersection with the opposite side, these line segments also define the orthocenter for the child triangle. Remember that not only are parent and child congruent but corresponding sides are parallel and corresponding angles are equivalent.
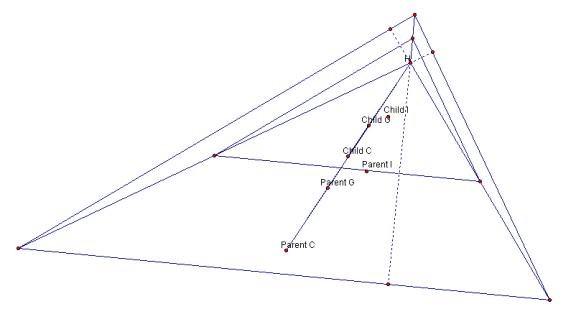
Since the parent and child triangle are congruent and co-aligned, the each may be view as a product of the linear transformation of scaling about the orthocenter. That is, each point on or related to the parent maps in one-to-one correspondence with a point on the child and visa-versa and are displaced a common scaling factor ( ½ going from parent to child) of there distance from orthocenter of the along linear trajectories emanating from the orthocenter. Since the parent Euler line intersects the orthocenters of both the parent and child triangles, the effect is that points are shifted along that line in the transformation.