
The Department of Mathematics Education
J. Wilson, EMAT 6680
EMAT 6680 Assignment #8:
Altitudes and Orthocenters.
Matthew Tanner
EMAT 6680
Write-up #8
June 18, 2004
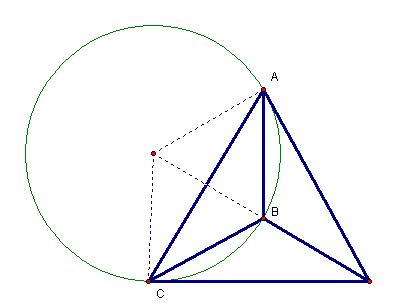
The Orthocenter of a Triangle is constructed by finding the intersection of any two altitudes of a triangle.
The Orthocenter of the triangle HAB is located at C. Likewise the Orthocenters of HBC and HAC are at A and B respectively. So the four vertices represent a closed set in which, if any three vertices are chosen to form a triangle, the remaining vertex is the Orthocenter.
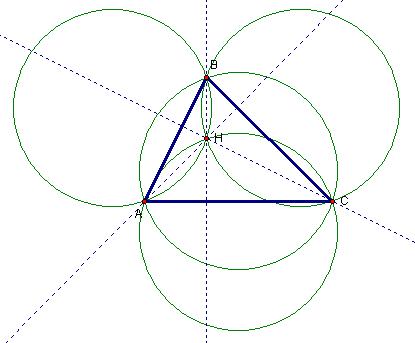
It is evident that obtuse triangles have exterior Orthocenters. Note in Figure 1 that the obtuse angle precludes the right angle vectors from ascending in the interior from the incident vertices. The inverse is also true all acute triangles have interior Orthocenters. Since no angle in an acute triangle is greater than 90°, the vertex opposite any side is within the 90° goalposts of that side. The intersection of the three sets of 90° goalposts corresponding to the three sides is the interior of the triangle so the Orthocenter is constrained to be interior.
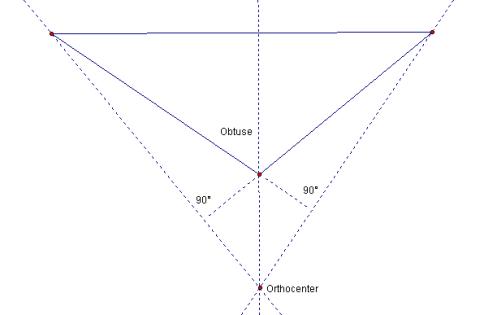
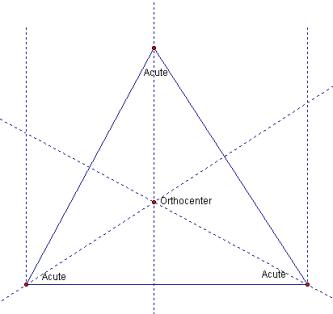
Figure 2
![]()
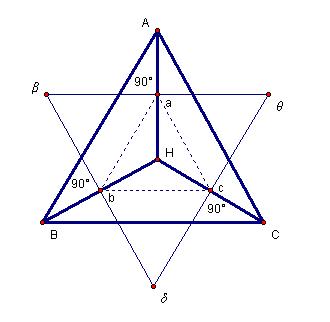
Furthermore, interior triangles incident to an interior Orthocenter must be obtuse. Note below that a and a sum to 90°. Likewise b and b are 90°. So a, a, b and b sum to 180°. Therefore, if BAC is acute, BAC is obtuse. Since the same condition is true of all the exterior vertices and the corresponding interior angles, all interior triangles incident on the Orthocenter must be obtuse.
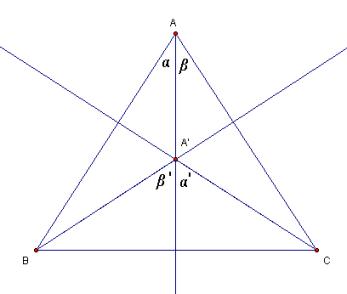
Figure 3
Next I claim and show by construction that the four inscribed Circumcircles are equivalent. First construct a triangle whose sides are perpendicular to and bisect the lines connecting the vertices of the original triangle and Orthocenter.

Figure 4
Note in Figure 4 that since the sides of the constructed triangle (call it the inverted triangle) are perpendicular to the segments connecting the vertices of the principle triangle to the Orthocenter (call them spokes), all points along the bisecting side are equidistant from the endpoints of the spoke that it bisects. So, for instance, the distance TA equals the distance TB and TB equals TC. Since TA equals TB equals TC, we know we can interpolate the three vertices with a circle (Figure 5).
Figure 5
Next we need to show that the midpoints of the sides of the inverted triangle are located at their respective junctions with the spokes. To do this, construct a triangle interior to the original triangle with vertices at the midpoints of the spokes (Figure 6).
Figure 6
Since the endpoints of the segment bc bisects BH and HC inheriting half their equivalent vertical components, it is clearly parallel to BC. The segments ac and ab are, likewise, parallel to their corresponding sides. Note that because bc is parallel to BC, it is perpendicular AH so it is parallel to bh likewise ab and ac are parallel to their respective inverted triangle opposite sides. This is especially noteworthy because it is this set of relationships that evoke the characteristics of the Orthocenter as distinct from any other point. Since ab is parallel to bh and ac is parallel to bd, ba and ah are both equal in length to bc and a is the midpoint. Similarly, b and c are the midpoints of their respective sides.
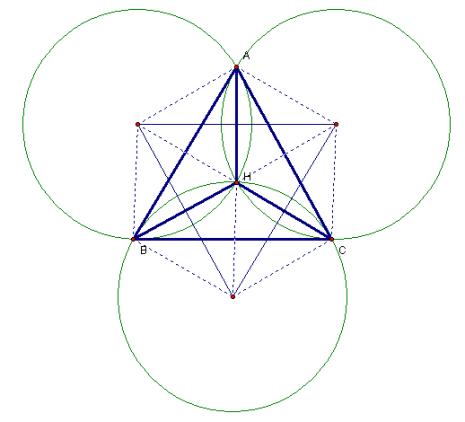
Figure 7
For the remaining circle, circumscribed on the vertices of the original triangle, we first show that the inverted triangle is equivalent to the original. Revisiting Figure 6, note that since the segment bc is parallel to BC and its endpoints bisect the spokes forming the triangle BHC, it inherits half the horizontal length of BC likewise with ac and ab with regard to AC and AB respectively. Recall that bh is twice the length of bc so it is parallel and equal in length to BC. This can be shown to be true of bd and dh with regard to their opposing sides as well. Since the sides of the inverted triangle are equal in length and parallel to each corresponding opposite side, it is equivalent. Either condition is sufficient for this conclusion.
Note from Figure 7 that we have already fixed the vertices of the inverted triangle all equidistant from the vertices of the original triangle and the Orthocenter. So we can circumscribe a circle equivalent to the earlier three on the vertices of the inverted triangle. Since we have shown the inverted triangle to be equivalent to the original triangle, we may translate it onto those vertices.
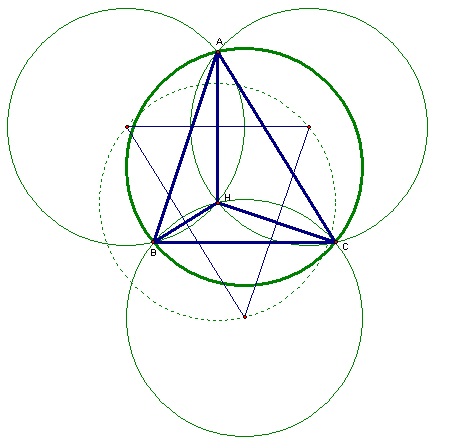
Figure 8
Returning to Figure 3 and recalling that BAC and BAC must sum to 180° and since the construction of the Orthocenter fixes A at the same right angle ascension from side BC as A, if A is moved to the position of A, then A moves to the previous position of A. Then same is true of B and C with respect to A. Note that this is consistent with the set of vertices {A,A,B,C} being a closed set in which if any three are chosen as the triangle, the remaining is the Orthocenter.
The nine-point circles attributable to any triangle and to the subcomponent triangle formed by any two of those vertices and the Orthocenter are equivalent.
Recall that we showed that the Orthocenter of a triangle has the property such that, taken along with the vertices of its constituent triangle, it comprises a closed set such that if any three members are chosen to form a triangle, the remainder is the Orthocenter of that triangle. Note that the full compliment of component triangles to ABC that is HAB, HAC and HBC can be derived by alternating each of the vertices A, B and C in sequence with the Orthocenter. All three cases reduce to the alternation depicted in Figures 9 and 10.
Figure 10 Figure 9
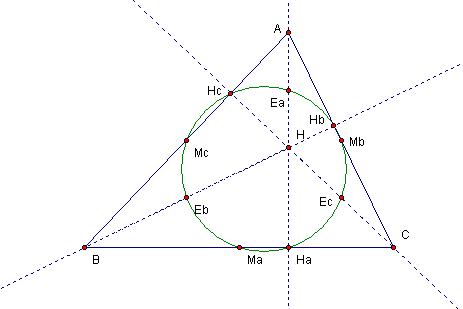
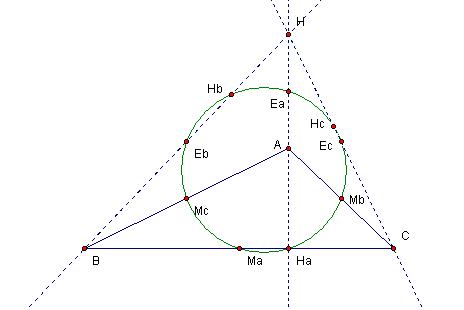
We know that when vertex A is moved to the location of the Orthocenter H, H moves to the previous location of A. Since Ma is the midpoint of segment BC and Ha is fixed by the perpendicular location of H and A which do not vary laterally in the alternation, neither is affected. When A and H alternate positions, the midpoints of segments HB and AB Eb and Mc respectively also alternate. Likewise with Ec and Mb. Since Hb is located at the right-angle junction of HbB and AC and Hc at the right-angle junction of HcC and AB, when A and H alternate segments HbB and AC and segments HcC and AB likewise alternate. The effect is that Hc and Hb also alternate. Finally, since H and A alternate positions and Ea is the midpoint of segment AH, the effect is that the position of Ea remains unchanged.
Since the identical location of any three points describe an equivalent circle and all points have identical location and so are consistent, we may conclude the circles are equivalent. The same hold true of vertices B and C. So we may conclude that any triangle and its component triangles incident on the Orthocenter have equivalent nine-point circles.