A Relation of Linear Functions and Their Product
By: Stephen
Bismarck
Find two linear functions f(x) and g(x)
such that their product is tangent to each of f(x) and g(x) at two
distinct points. Discuss and illustrate the method and the results.
h(x) = f(x).g(x)
I knew that the two functions had to have opposite slopes (one
positive and the other negative).
So I started off with
f(x) = nx +
n and g(x) = -nx + n
h(x)
= (nx + n)(-nx + n)
I did this because I want to see if all the constants and
coefficients were the same.
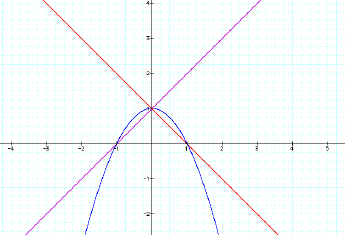
This for n = 1 and I observed
that the bigger n got the further away the vertex of the parabola got from the intersection
of the lines.
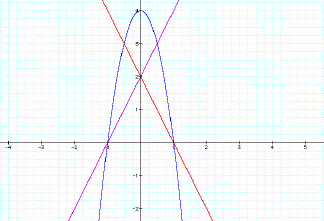
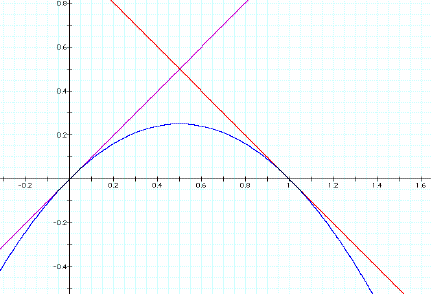
This is for n = 2. So from observing that I thought about values smaller than n = 1 and this is where I got my first solution.
This is for n = .5 but how do I know it’s a solution. Well since we want each line to be tangent to the product of the lines, each must only touch the parabola. So I set each linear equation equal to the product of the lines.
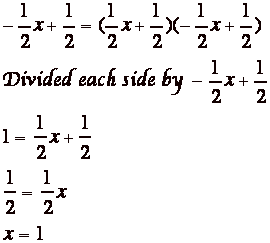
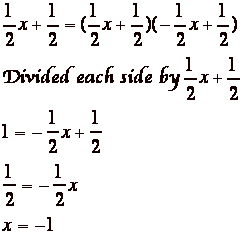
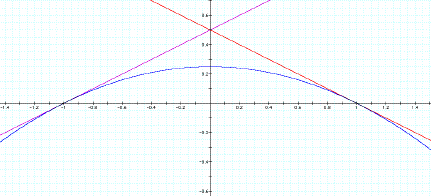
As you can see from the
picture and if you plug the values for x back into the equation, the distinct
points are (1,0) and (-1,0).
So my first solution is
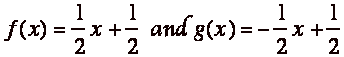
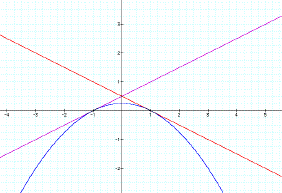
For the second solution I tried to keep f(x) constant and change
g(x). I decided to pick f(x) = x
and g(x) = -nx + n so h(x) = x(-nx +n).
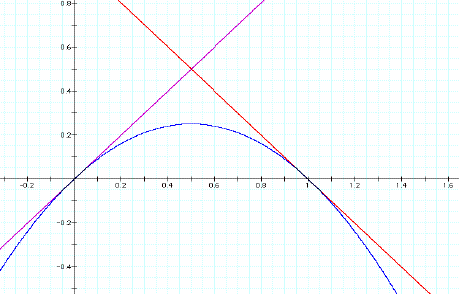
I found this graph for when n = 1. It looks like the tangents are at (0,0) and (1,0). I decided to use some calculus to
determine if they are tangents.
I took the derivative of the product of the two lines, h(x) =
x(-x+1), and got h’(x) = -2x + 1 so I plugged in the x values of 0 and 1
from the points that I thought might be where the tangents are.
h’(0) = 1 and h’(1) = -1
So to find the equation of the tangent line I plugged in the slope
and a point on the graph of h(x) and got y = x and y = -x +1. This supports my hypothesis that f(x) =
x and g(x) = -x + 1 are solutions.
The two solutions that were found to this problem were
1. 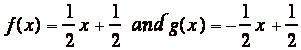
2.
f(x) = x g(x) = -x +
1 and h(x) = x(-x + 1)
________________________________________________
1.

2.