

I intend to explore some mathematical concepts behind the production and consumption of electricity and how it makes it travels from the generators to your house. I have been interested in electricity for a while now, my father worked for Consolidated Edison (Con-Ed) for over 20 years and is currently working for Orange & Rockland Utilities. If you don't know about either of these two companies, you're not from the New York, New Jersey area. Basically they are the electric companies for New York City and surrounding areas. Growing up in that environment I learned a lot of electrical engineering from my father and learned some more on my own. Most of the materials that I will be presenting on this page I want to thank my father, Fred Bismarck for providing me.
As I was researching how electricity works and how to calculate such things as resistance, voltage, and current, I found that most of the calculations were pretty basic, many having to do with setting up ratios. So, I'm going to skip that section and get to the good stuff, the production of AC electricity.
AC Electricity
Electromagnetism
AC electricity has a lot to do with electromagnetism. So let me give you some history behind it. In 1819, Hans Christian Oersted, discovered that a field of magnetic force exists around a wire carrying an electric current. You many have seen this concept done in a school science fair. If you take a battery and run a wire from the negative side to the positive side passing through a piece of cardboard with iron filings on it, the iron filings will make rings that represent the magnetic field. The larger he current the larger the field.
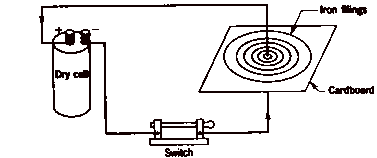 *
*Electromagnetic Induction
Now this brings us to induction. In 1831, Michael Faraday is credited with the discovery of the basic principle underlying the operation of AC machinery. Basically he found out that if a conductor cut across lines of magnetic force a voltage would be induced across the ends of the conductor.
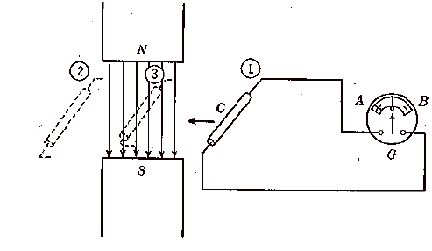 *
*
The only problem is that a conductor must cut 100,000,000 lines of force per second to induce 1 volt. One of the solutions to this problem was to have the conductor rotate. in the pictures below the conductor is rotating counterclockwise and the magnitude of vectors AD, BE, and CF are equal, they are actually the distance from O to C. The motion is directly across the lines of force and produce the maximum number of cuttings and maximum voltage Emax.
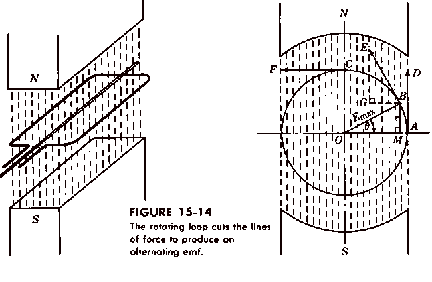 *
*
As you can see this forms a right triangle so trigonometry can be used to find out what the maximum voltage is. The symbol e represents the instantaneous voltage.
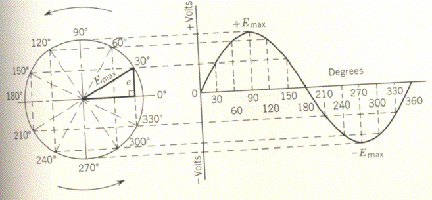 *
*
Transformers
Before we can talk about transformers we must talk about coils. If you put a coil into the wire where current is flowing, for a AC source, you'll find that the coil expends some of the voltage. This happens because the moving lines of force cut the turns of the coil. These cuttings induced a voltage in the coil and in the direction so as to oppose the original voltage. This is called a back emf. The amount of the back emf depends on the number of cuts of the line by the conductor.
The primary purpose for transformers is to decrease the amount of voltage from one place to another. It is cheaper to transmit electrical energy at high voltages than low voltages because of the smaller loss of power in high voltage lines. A transformer may have receive a transmission of 220,000 volts from a power plant and have to decrease that to 120 volts for an ordinary home, how do they do that? Basically it is using the idea of coils that I stated above. The figure below is of a very simple transformer but it gets the point across. The core is many times made out of a highly magnetic material, although cardboard and ceramics are used for the cores of some radios and televisions.
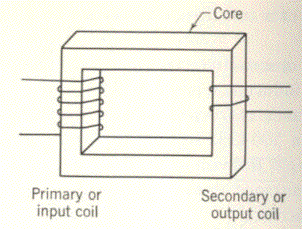 *
*
The current comes into the transformer from the primary or input coil. The changing magnetic field is carried by the core to the secondary coil, where it cuts across the turns in the coil. The number of coils in each line determine what the voltage will be.

* All figures where taken from Basic Mathematics For Electricity and Electronics by Bertrand B. Singer