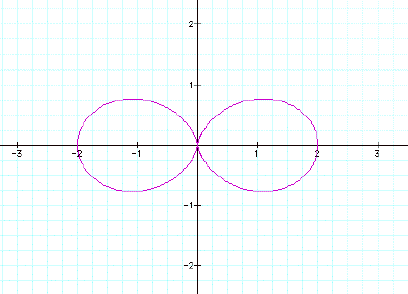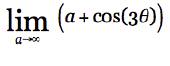Explorations of the
n-Leaf rose
By: Stephen Bismarck
To come up with a "rose"
mathematically, you need to use polar equations. In polar equations
your variables are q (theta) and r (radius) which can be converted
to the x and y cooridanites that we are all used to by x = r cos(q)
and y = r sin(q).
Well lets get back to
the rose issue.
The basic n-leaf rose
comes in the for r = a + b cos(kq), where a = b.
So let's say that a =
1 so b = 1 and the equation will be r = 1 + cos(kq)
but we have not picked a value for k, so let k = 2, the equation
is now r = 1 + cos(2q)
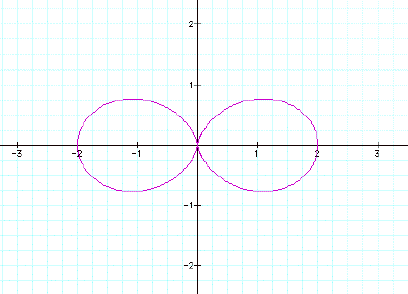As you can see this "rose"
has 2 leafs.
Another example is r =
1 + cos(3q), how many leafs do you think this "rose"
has?
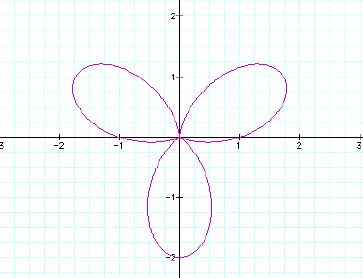Look at this, there are
3 leafs. It seems like the number for k determines the number
of leafs that you will see for this "rose".
Instead of having a = b, lets look
at all the different case for a and b. There is when a > b
and when a < b.
When a > b
For intstance we looked at r = 1 + cos(3q), in this case a and b =1 so change a
to 3 and keep b =1 and lets look at the graph.
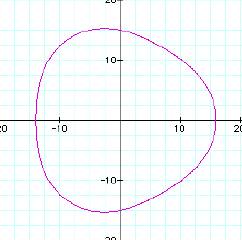As you can see the inside
of the rose is unfolding out. Let's look at a more exterme case,
when a and be are much further apart.
Let a = 15 and b =1, what
is going to happen to the graph now?
The graph is getting bigger
now expanding out to 15 on both the x and the y axis and it also
looks like it's getting closer to a circle.
Why is this happening?
Well there is a few ways
you can think of this. One way is just understanding the equation
itself.
r = 15 + cos(3q),
the cos(3q)'s values will only range from -1 to 1 no matter
what values you put in for q. The 15 is doninating the equation only
being varyed by one and that's why the graph has an egg shaped
look. So if you pick a = 100 the graph will look more and more
like a circle with radius 100.
The other way of looking
at it would be more of a calculus concept. We are increasing the
a value and keeping the b value the same sort of like looking
at a limit as this equation aproachs infinity.
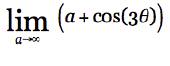Like what was determined
in the other way is that the cos(3q)'s values will only range from -1 to
1, so in this limit it is like a constant. a is aproaching infinity
so r = infinity. That graph is a huge circle with radius infinity.
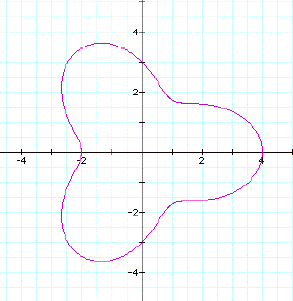
So the other case is when
a < b.
So let's say that we have
the equation r = 1 + 2cos(4q)
Does not look the rose
is unfolding like before but forming more pedals, the same amount
that the k value is.
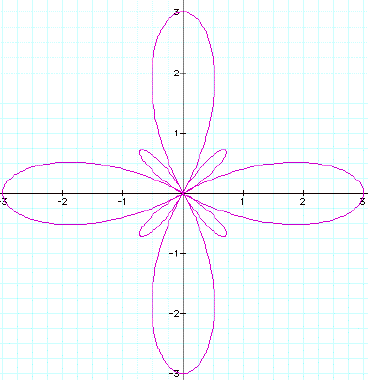
Let's look at one that
k is odd like r = 1 + 2cos(3q).
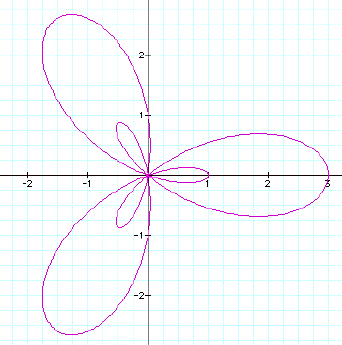When k is odd it looks
like the "extra" pedals are inside the other pedals.
RETURN