 Fibonacci Numbers
By: Stephen Bismarck
Fibonacci Numbers
By: Stephen Bismarck
The fibonacci numbers are a recursive
sequence with the first two values as one. Recursive sequences
are constructed by doing a certain operation to the terms before
and repeating the process infinity.
With the fibonacci sequence you add
the previous two terms together and the result is your next term
in the sequence.
Example: 1, 1, 2, 3, 5, 8, 13, 21,
34....
You can do this process to any two
given numbers. For example, if you start with 3 ,4
3,4,7,11,18,29,47....
I come back to some ideas like that
later.
If you haev heard of fibonacci numbers
then you most likely have heard of the golden ratio.
The golden ratio is no more than the
limit of each consecutive fibonacci number.
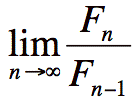 And the answer to the limit is
And the answer to the limit is 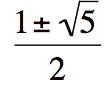 But how did I get that?
To show how to get the golden ratio we must agree with
one big axiom, that the limit exists.
But how did I get that?
To show how to get the golden ratio we must agree with
one big axiom, that the limit exists.
 Proof: Ever consecutive fibonacci numbers
are relatively prime
Proof by contraction
Proof: Ever consecutive fibonacci numbers
are relatively prime
Proof by contraction
 Since d is not greater than 1 and d
can't be negative(fibonacci numbers are positive), it must be
1.
So consecutive fibonacci numbers are
relatively prime.
Since d is not greater than 1 and d
can't be negative(fibonacci numbers are positive), it must be
1.
So consecutive fibonacci numbers are
relatively prime.
Here's a computer program I made that
will give you any fibonacci number. all you have to do is tell
it which one you want.
For example n = 6 the 6th fibonacci
number is 8
Fibonacci
Numbers
Let us look back at the other sequence I should you
3,4,7,11,18,29,47....
Let's take a different aproach and
look at these numbers in excel
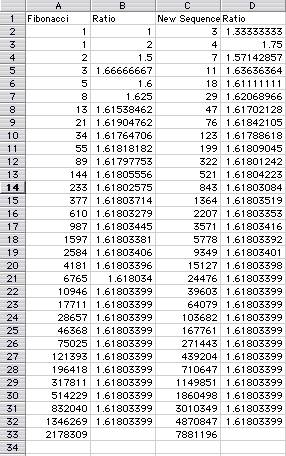 Here's the Excel worksheet for you
to look at
Fibonacci
Excel
As you can see the ratio of the fibonacci
numbers and the ratio of the new sequence are about the same at
line 32.
And from earlier we know what the ratio
is
Here's the Excel worksheet for you
to look at
Fibonacci
Excel
As you can see the ratio of the fibonacci
numbers and the ratio of the new sequence are about the same at
line 32.
And from earlier we know what the ratio
is 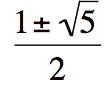 which is about 1.61803399...
The derivation of the golden ratio
doesn't have to do with starting with 1,1 like we see so many
times.
You can start with any two numbers
just use the same pattern.
Every time the ratio of each consecutive
term is aproaching the golden ratio.
RETURN
which is about 1.61803399...
The derivation of the golden ratio
doesn't have to do with starting with 1,1 like we see so many
times.
You can start with any two numbers
just use the same pattern.
Every time the ratio of each consecutive
term is aproaching the golden ratio.
RETURN


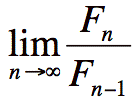
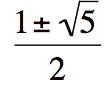



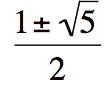 which is about 1.61803399...
which is about 1.61803399...