Tangent Circles

 

By: Stephen Bismarck

---

 

Given two circles find a circle tangent to both. This might be hard to imagine so here is a picture of what I'm talking about.

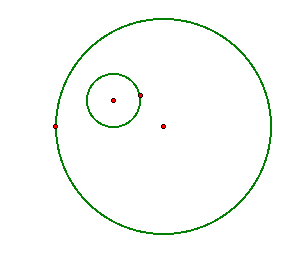This is the case where one circle is disjoint inside the other, you could have two circles that are disjoint outside of each other too.

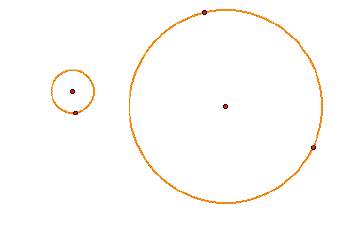How many tangent circles are there for these pictures?

 

That was sort of a trick question, there are an infinite amount of tangent circles.

To figure out one tangent circle, there has to be a given point on either of the circles that will be on the tangent circle also.

Here are two GSP scripts that enable you to get tangent circles.

Tangent Circle

Tangent Circle incompasing both given circles

 

If there is a circle inscride the other, like in the first picture, what is the locus of the center of the tangent circles?

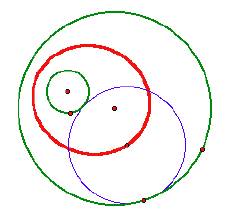The red trace is the locus of the center of the blue tangent circle. As you can see the locus is an ellipse with foci at the center of the two original circles.

 

When the circles are disjoint the result is much different.

 

 

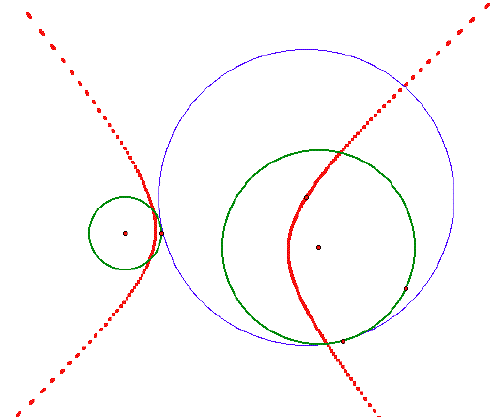The locus in this case turns out to be a hyperbola with the foci again the centers of the two given circles.

I have found that it does not matter what size the circles are, just if they are disjoint outside.

 

 

 

 

 

 

 

RETURN