Investigation of the Relationships Between
Orthocenters, Incenters, Circumcenters and Centroids
By: Denise Natasha Brewley
To begin this investigation, the construction of the Centroid, G, the Orthocenter, H, and the Circumcenter, C of triangle ABD was done. For more detail of how each construction looks please look at the following respectively:
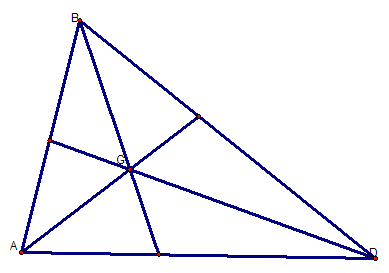
The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
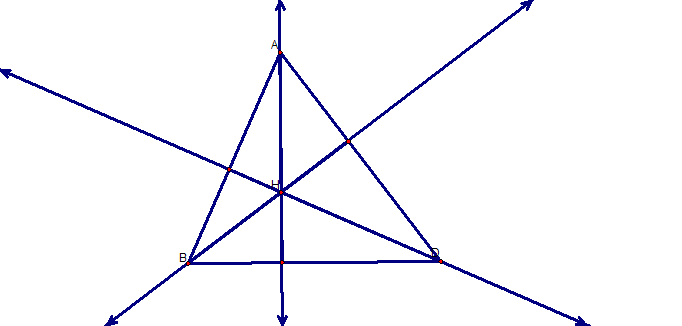
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
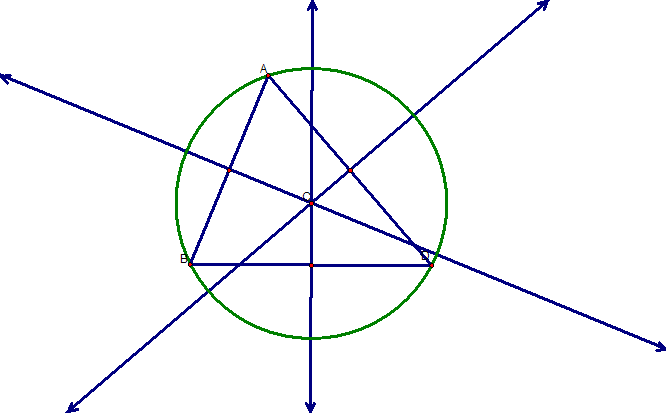
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from the two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle.
Last, the construction of the incenter, I, of triangle ABD was also done. For this construction, we used the fact that a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector. The three angle bisectors were found. At their point of intersection, a perpendicular line was formed between the intersection point and the base of the triangle. The distance from the intersection point to the base of the triangle where the perpendicular line passes, is the radius of a circle that is inscribed in the triangle. The center of this circle is the incenter, I.
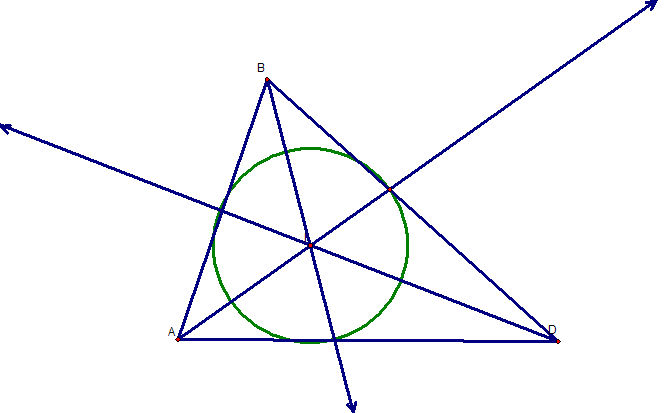
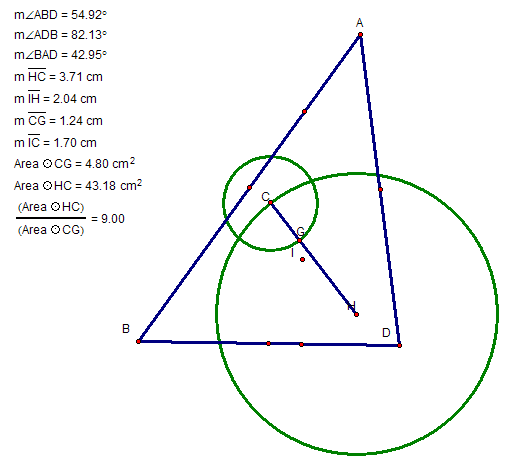
All four of these points were placed in triangle ABD and a line segment, HC was formed. This is depicted below. Notice that if each angle's measure is less than 90 degrees, the incenter is on the line segment HC.
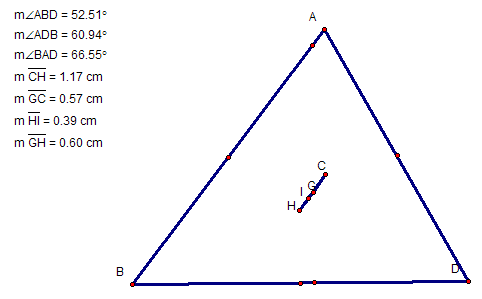
When triangle ABC is an obtuse triangle, greater than 90 degrees, line segment HC extends outside of the triangle. But also notice that the measure of GC is always equal to two thirds the measure of HC.
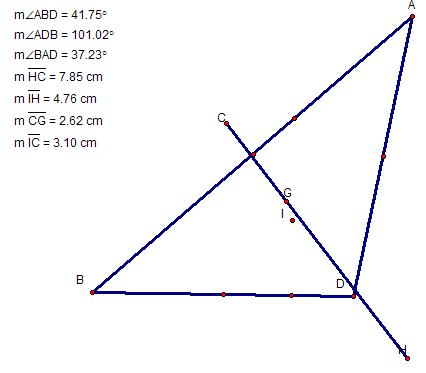
Let's say we construct two circles one with radius HC and another with radius GC and find their areas, the ratio of the areas are 9:1 respectively. This can be shown by first considering that CG = HC/3. The area of each circle is A=pr2. It follows that A=p(HC/3)2 = p(CG)2 which is equivalent to p(HC2/9) = p(CG)2. Multiplying both sides of the equation by 9/p(CG)2 gives us the desired proportion that we want. And this always holds true for the euler line segment.