Investigation of Altitudes and Orthocenters
By: Denise Natasha Brewley
I begin this investigation by constructing triangle ABC. I then construct the orthocenter H of the triangle ABC. Notice here that the orthocenter is inside of triangle ABC. Now consider the following -- What if I divide triangle ABC into three triangles, HBC, HAB, and HAC. Where will the orthocenter be for these triangles?
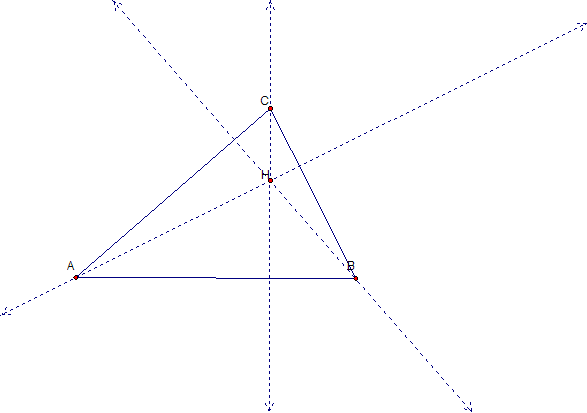
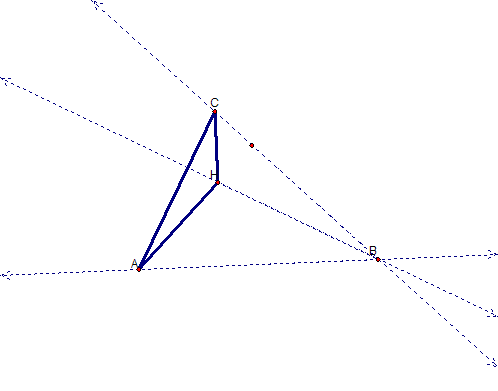
In thinking about the posed question, I constructed and highlighted triangle HBC. Notice that when I found the orthocenter of triangle HBC, it was the point A, which is one of the vertices of triangle ABC. Also notice that the orthocenter is located outside of triangle HBC, which is different than our original case where H was inside of triangle ABC.
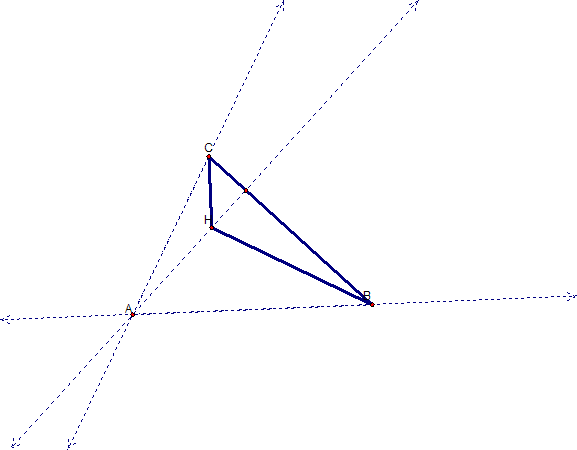
I then constructed and highlighted triangle HAB and constructed its orthocenter. In this case the orthocenter turned out to be the point C, which was again outside of the triangle HAB. So it looks like we can make a conjecture about the last triangle, in locating its orthocenter. For triangle HAC, it will probably be point B.
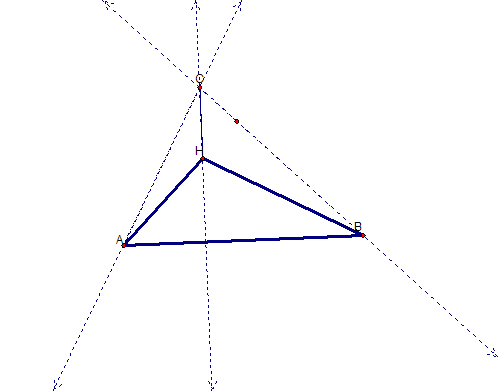
Well it looks like we are correct! Once again the orthocenter is outside of triangle HAC.
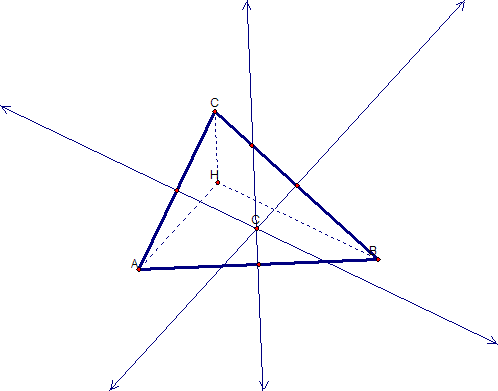
Now, let us take a look at the circumcenter of triangle ABC. Just as a reminder of how I got this construction, I first found the midpoints of line segments, AC, CB, and AB. I then construct the perpendicular lines through the midpoints. The circumcenter is the intersection point of those three line segments. In this case that intersection is the point C.
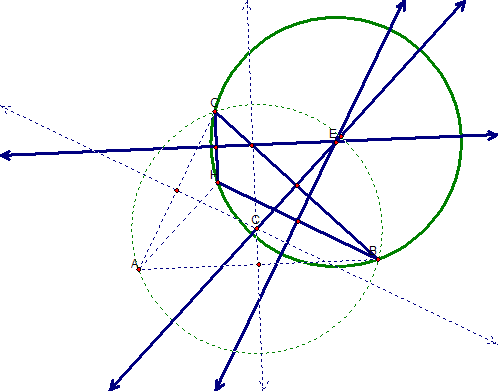
I now want to begin to construct the circumcircles for the four triangles that explored previously, ABC, HBC, HAB, and HAC. I start off by constructing the circumcircle for triangle ABC. Notice here that the circumcircle goes through all of the points of triangle ABC.

Repeating the process, I now construct the circumcircle of triangle HBC. Note that I left the circumcircle constructed from triangle ABC intact -- it is indicated by the dashed line. I will make some conjectures after I have completed the construction. The circumcircle for this triangle is indicated as circumcircle E.
Again, I continue with this process of constructing the circumcircles of the triangles. This time, I make the construction for triangle HAB. Again, I will leave intact the other two circumcircles that were constructed. The circumcircle for this triangle is indicated as circumcircle M.
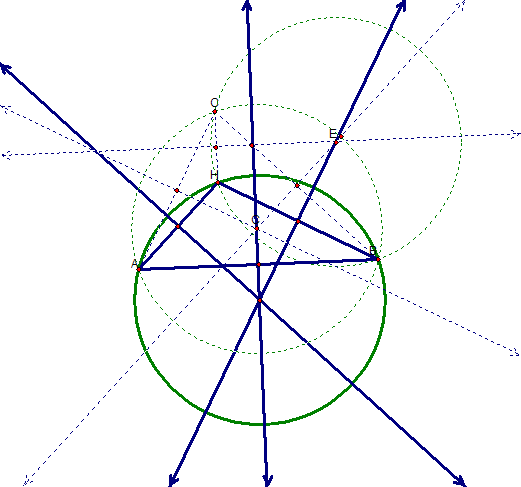
I are finally done with the last construction. For triangle HAC, we create the circumcircle for this as well. Notice that I have left intact all of the circumcircles that we previously constructed. The circumcircle for this triangle is indicated as circumcircle O.

For clarity, I removed all of the perpendicular lines and indicated the original triangle ABC in bold. Two of the Circumcenters name have been changed from the previous construction. I am now ready to explore.
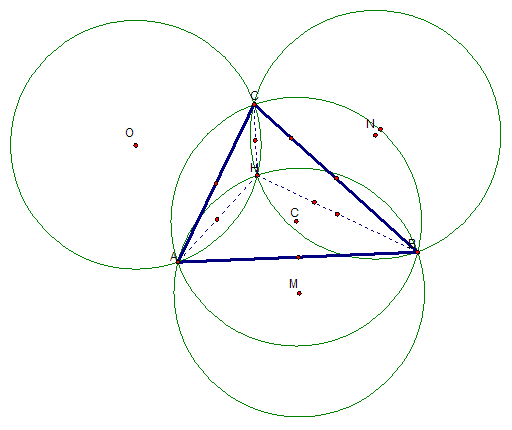
In triangle ABC, let angle A be a right angle, then the orthocenter H of triangle ABC overlaps the vertex of triangle ABC. This is interesting because point A is the circumcenter of triangle HBC. So this means that the orthocenter, H, and the circumcenter, A, are the same when angle is 90 degrees. If I continue to explore this idea for different cases, we will get the same results. That is, when angle B and C are right angles respectively, then the orthocenter H of triangle ABC will overlap the vertex of triangle ABC, respectively as well. So this means that the orthocenter, H, and the point B is the circumcenter of triangle HAC. The same goes for the point C is the circumcenter of triangle HAB.
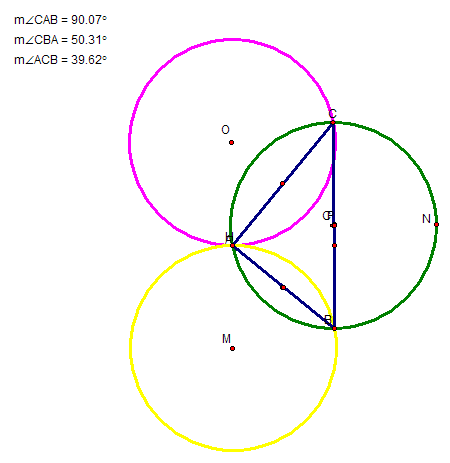
If triangle ABC is an equilateral triangle, simultaneously with both its orthocenter point H and its Circumcenter, point C overlapping, then notice that all of the Circumcenters of triangles HAC, HAB, and HBC - namely point O, M and P are all points that lie on the circumcircle for ABC.
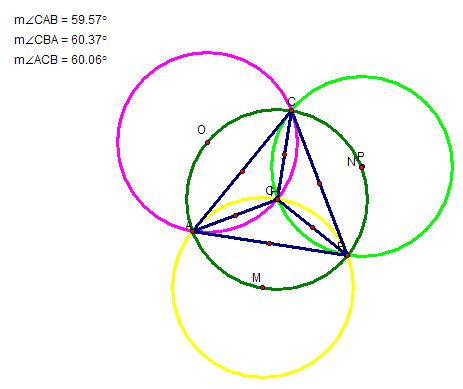
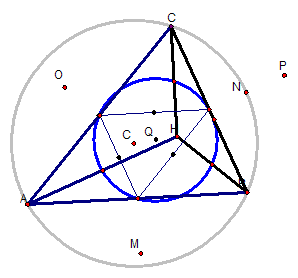
To end this investigation, I go about constructing The Nine Point circle. First, I took the sketch that I had drawn previously and constructed a medial triangle of the original triangle ABC. I then found the orthocenter of the medial triangle and called it point Q. Next, I constructed a circle by center with point Q as center to any midpoint of the original triangle ABC. The sketch below illustrates the Nine Point Circle which is a circle that passes through the midpoints of a triangle's edges, the midpoints of its perpendicular segments, and the feet of a given triangle's perpendiculars.