
Lisa Brock
Assignment 11
The Effect of k on r=a+bcos(kq) and r=bcos(kq)
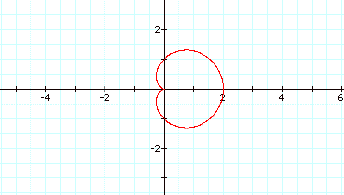
Lets investigate the polar
curve r=a+b cos (kq). Let begin by looking at the graph when
a=b=k=1.
![]()
Now lets hold a and b at 1
and vary k. Lets look at k=2, 3, 4
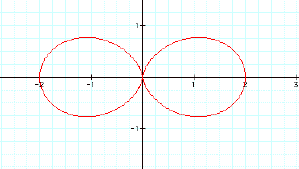
![]()
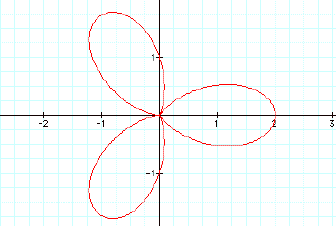
![]()
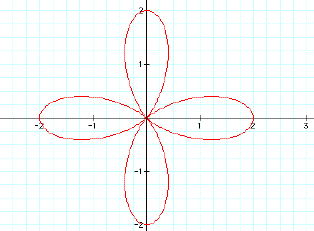
![]()
The number of petals on
the graph is the value of k. Just
to be sure, lets look at k=10 and k=100.
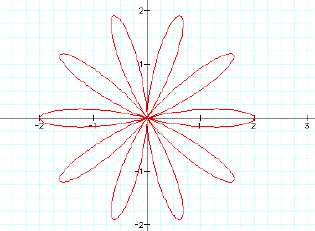
![]()
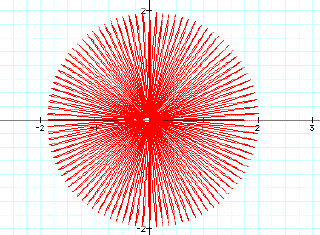
![]()
As you can see, this
relationship holds for all integer values of k. This is called the n-leaf rose because there are n petals or
leaves when k=n.
Lets see what happens when
we eliminate a. Then our equation
is r=bcos(kq). Lets begin by looking at the graph when
b=k=1.
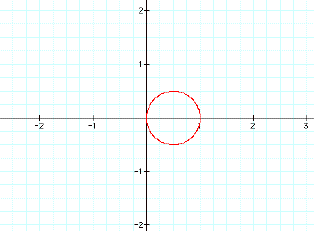
Now lets hold b at 1 and
vary k. Lets look at k=2,3,4.
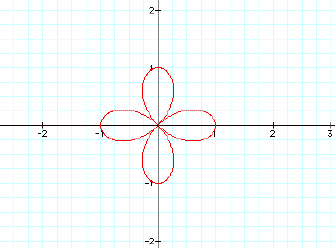
![]()
![]()
![]()
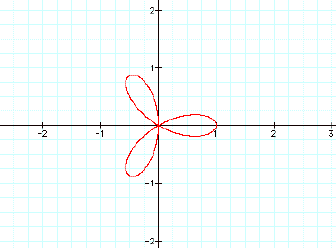
When k=2, there are 4
petals. In this case, the number
of petals is 2k. Based on this, I
expected that there would be 6 petals when k=3. But there were only 3 petals. In this case, the number of petals is k. When k=4, there are 8 petals. Again the number of petals is 2k. This leads me to believe that when k is
even, the number of petals is 2k.
When k is odd, the number of petals is k.
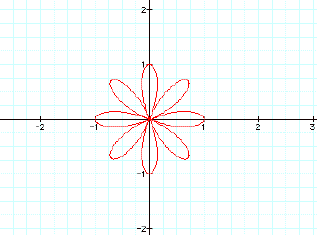
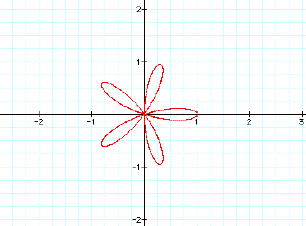
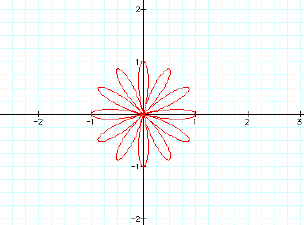
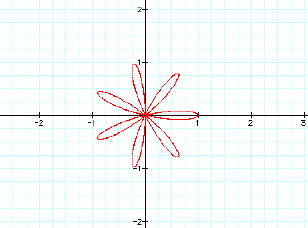
Lets look at k=5,6,7 to
see if this theory is true.
![]()
![]()
![]()
The theory appears to hold
true. So for the polar equation
r=bcos(kq), the are k petals when k is an even integer and
2k petals when k is an odd integer.
Lisa Brock’s Home Page