Lisa Brock
Assignment 3
The Affects of a, b, and c on 
To best examine the
affects of a, b, and c on the curve 
, we
must examine each variable individually while holding the others constant.
Let's begin with a. Let b = 1 and c = 1. This results in the
equation 
. Graph this equation for different
values of a.
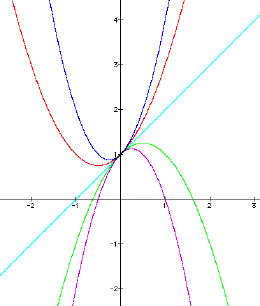
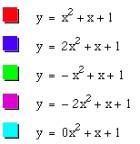
Each graph goes through
the point (0,1). When a = 0, the graph is a line instead of a
parabola. When a = 0, the 
term becomes zero, turning the equation
into a linear equation. When a is positive, the graph is concave up. When a is negative, the graph is concave down. As the absolute value of a increases the parabola becomes more steep and
narrow. Also, the position of the
vertex changes as a is varied.
Therefore, a determines the direction of concavity, the
steepness of the parabola, and the position of the vertex.
Now let's take a look at b. Let
a = 1 and c=1. This results in the equation 
. Graph this equation for different
values of b.
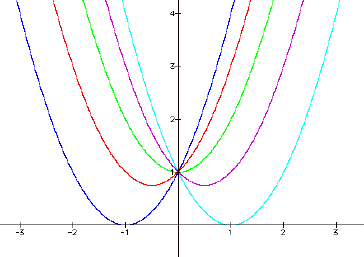
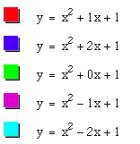
Each parabola goes through
(0, 1). Each graph is concave
up. Each graph is of equal
steepness. The vertex shifts as b changes.
As b increases in the
positive direction, the graph shifts farther to the left. As b increases in the negative direction, the graph
shifts farther to the right.
Therefore, b has an affect on the position on the vertex. Since the value of a also has an affect on the position of the vertex,
the values of both a and b will determine the position of the vertex.
Let's see what affect c
has on the graph. Let a = 1 and b
= 1. This results in the equation 
. Graph this equation for different
values of c.
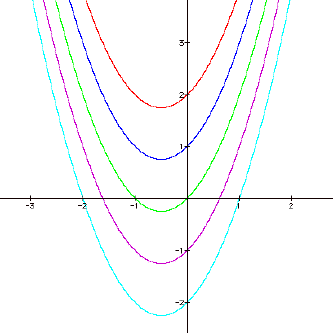
Each graph is concave
up. Each graph is of equal
steepness. The vertex has shifted
vertically but not horizontally.
Therefore, c affects the y-coordinate of the vertex.
In summary, a, b,
and c all determine the
position of the vertex. c appears to affect only the y-coordinate of the
vertex. b appears to affect both coordinates of the
vertex. a appears to affect both coordinates of the
vertex. a also determines the direction of concavity and the
steepness of the parabola.
Return
to Lisa Brock's Home Page