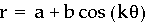
We are going to investigate the following polar equation:

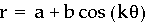
First we graph the equation where a,b, and k are all held constant (equal to 1) and theta is between 0 and 2 pi.

Now we will hold a and b constant and vary the values of k.

When k=2, we get the following graph.

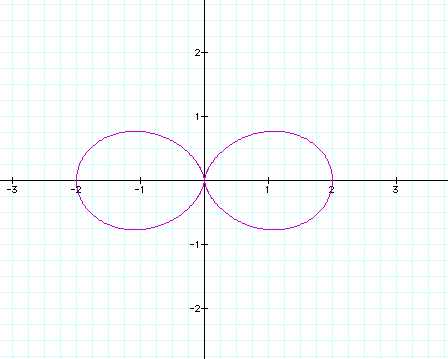
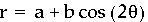
Notice that there are 2 leaves on the graph when k=2. The leaves cross the x-axis at the origin and at the points (-2,0) and(2,0).

What happens if we hold a and b constant and let k=3?

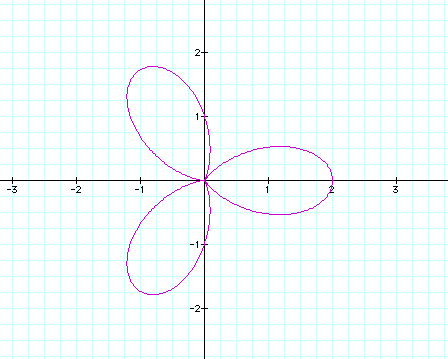
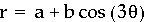
Now there are 3 leaves in the graph with the intersection at the origin.

What about when k=10?

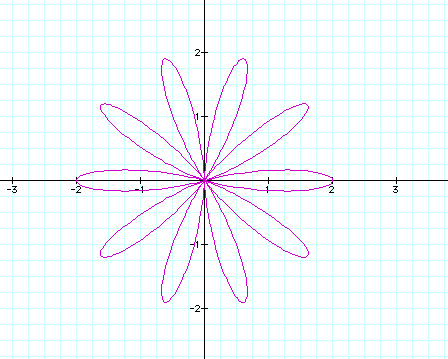
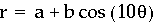
As you probably expected, there are 10 leaves. It appears that k determines the number of leaves for each polar function.

Just to be sure, we can graph the function when k=100.

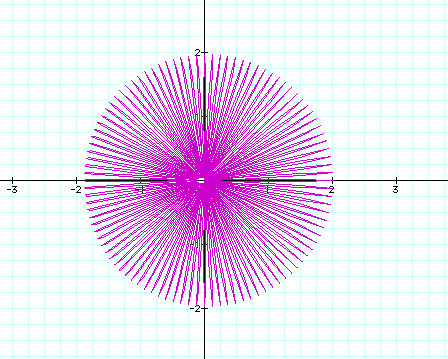
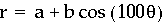
Though they are very small, there appears to be 100 leaves. Therefore, when a and b are equal, and k is an integer, the function forms an "n-leaf rose".

Now, we want to investigate the polar equation without a.

---

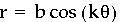
We will look at several equations where b is held constant at 1 and k is altered.

When k=1,

Notice that there is only one leaf. Does this imply that k also determines the number of leaves for the function:

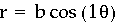
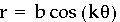
When k=2,

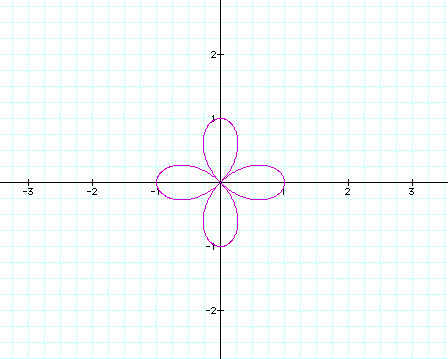
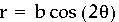
We were expecting there to be two leaves, but there are four. Maybe the number of leaves is equal to 2k.

Let's try k=3,

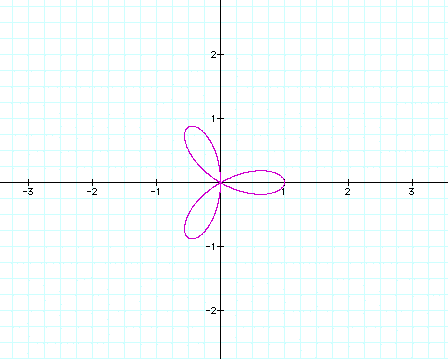
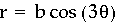
Here we were expecting six leaves, but instead we have three. So possibly the number of leaves is equal to 2k for even numbers and k for odd numbers. Let's try this for a larger even and odd number.

When k=10, we have an even number and 2(10)=20. Are there 20 leaves? Yes!

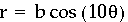
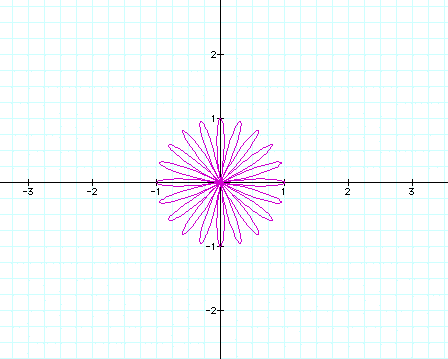
What about when k=11? Here we have an odd number equal to 11 and we have 11 leaves...so our theory works!

For the final part of our investigation, we will take the equation and replace the cos with sin.

Again hold the b constant and alter the values of k. First, graph the function when k=1.

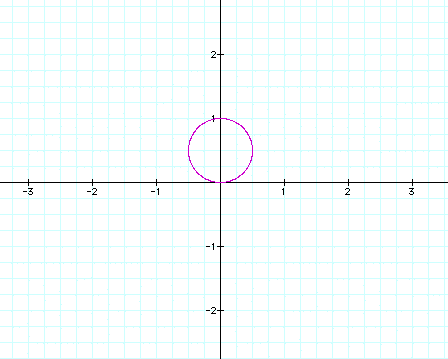
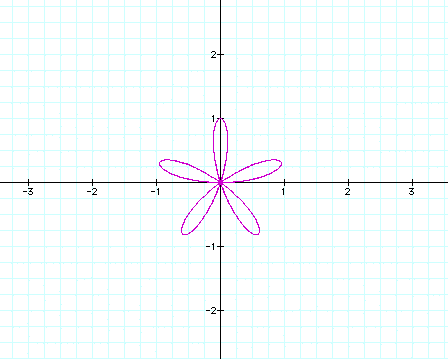
Here, there is one leaf. My first assumption is that k=number of leaves....However, what happens when k=2?

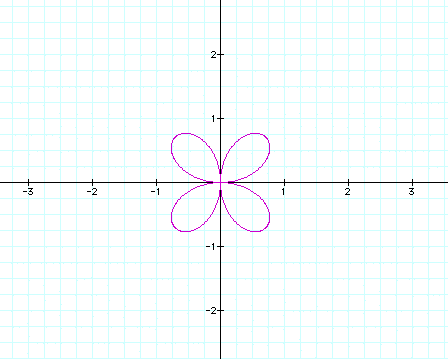
Here, I was expecting 2 leaves, but there are four. Now, I suspect that we will have the same properties as before when using the cosine function. When k is even, the number of leaves is equal to 2k. When k is odd, the number of leaves is equal to k. Is this true?

Let's try k=5. Five is an odd number, so there should be five leaves. Are there five? Yes!

---

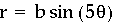
Now let's try k=6. Six is an even number and 2(6)=12. Are there 12 leaves? Yes!

---

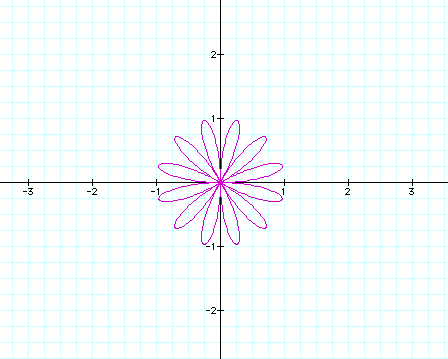
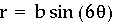
This concludes my investion of polar equations. There are numerous other activities you could perform. Feel free to explore.

Return