We are given the equation y=ax^2+bx+c=0 and asked to plug in different values of a, b, or c as the other two are held constant. Then we are asked to discuss any patterns that can be followed.

*

*

*

*

*

*

*

Notice that each graph goes throught the point (0,1) and appears to be a parabola except when a=0 where it is a line. If a is positive, the graph is concave up. If a is negative, the graph is concave down. Recognize that as the absolute value of a increases, the parabolas become skinnier and more steep. The position of the vertex also changes.

Next, I will let b vary and hold a and c constant.

*

*

*

*

*

*

*

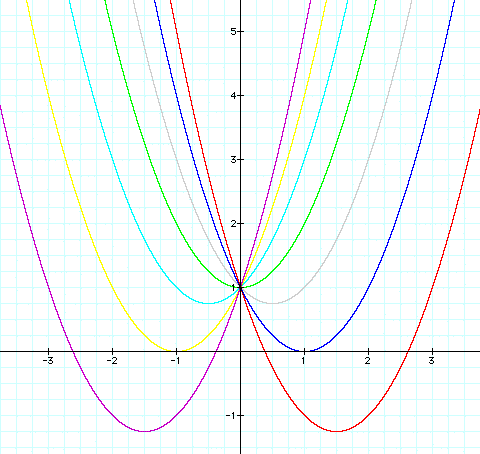
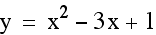
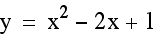
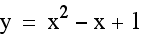
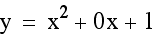
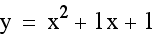
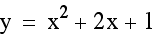
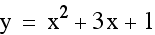
Notice that the vertex shifts as b varies. Also, the graph shifts to the right as b increases in a negative direction and the graph shifts to the left as b increases in a positive direction.

Lastly, let c vary while a and b are held constant.

*

*

*

*

*

*

*

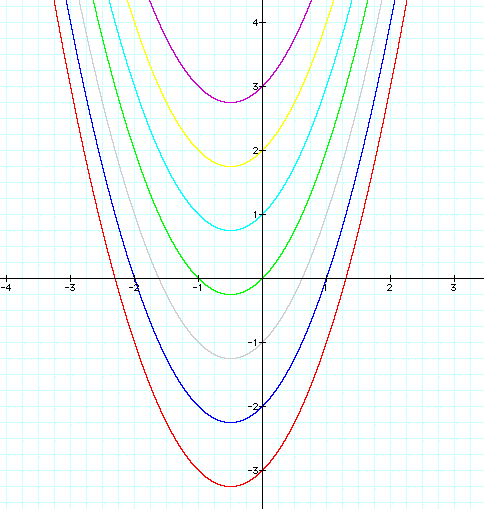
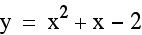
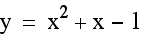
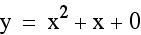
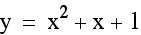
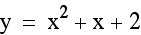
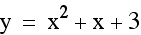
Notice that as c varies, the vertex is shifting up and down...therefore c is changing the y coordinate of the vertex.

To conclude, a, b, and c affect the position of the vertex. A and B affect both the x and y coordinates of the vertex. C appears to affect only the y coordinate of the vertex. In addition, a also determines the direction of concavity and the steepness of the parabola.

Return