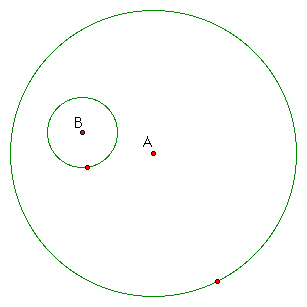
Given two circles and a point on one of the
circles, construct a circle tangent to the two circles with one
point of tangency being the designated point.
Start out with a large circle of any size with one arbitrary point on this circle. Label the center A. Then construct a smaller circle inside this large circle and place a point on it as well. Label the center B.

Next construct a line through the center of the large circle to the arbitrary point C on the large circle. Then, construct a segment from the center of the small circle to the point on the large circle.

Now construct a circle using the radius of the small circle and point C on the large circle.

Next construct a segment from the center of the small circle to the intersection of the new small circle with center C and the line that extends through points A and C to find the midpoint. From the midpoint, construct a line perpendicular to the segment you just created.

Mark the intersection where the perpendicular line crosses segment AC. You can use this intersection as the center of your circle that is tangent to the two circles. The radius will be from the new intersection to point C.
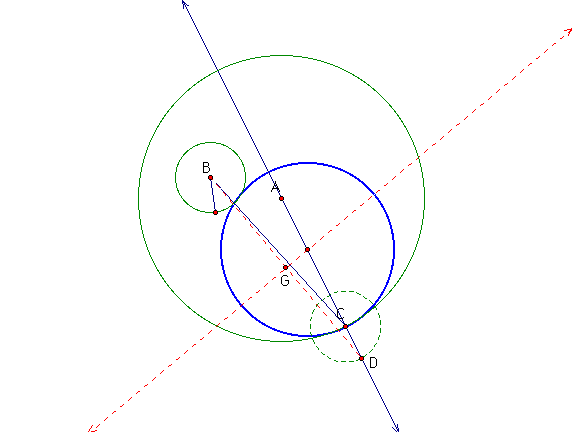
Therefore, the blue circle is tangent to the
first two circles. Click here
to use the script tool. Be sure to move the circles around. Notice
that no matter where you move the circles, the blue circle will
always be tangent to both of them.
Let's check our work. Is the blue circle really the correct tangent circle?
There is a relationship that exists concerning the center of the tangent circle. The center of the tangent circle that you found (the blue one) lies along the perpendicular bisector of the base of an isosceles triangle. The tangent circle's center is formed at the vertex of an isosceles triangle that has two equal sides that represent the distance from:
The center of the smaller circle you began with to the center of the tangent circle.
The point of intersection outside the large circle on the green circle to the center of the tangent circle.
As you can see below, these two sides form the equal side lengths of an isosceles triangle. These sides are represented by line segments HB and HD. Both of these lengths are equal to 4.46cm. DB has a different length and forms the third side of the isosceles triangle with a length of 8.5cm.
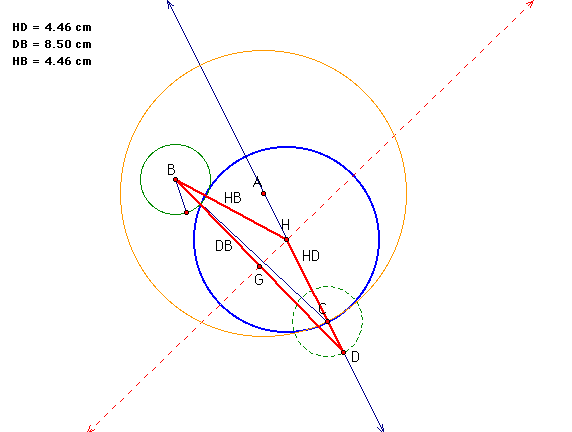
So it appears that we have found the correct
tangent circle. YES!