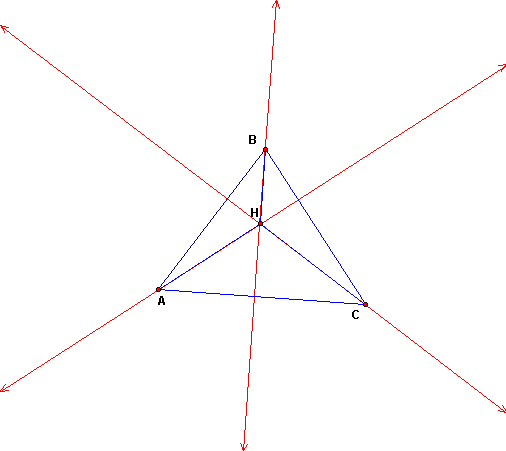
1. Construct any triangle ABC.

2. Construct the Orthocenter H of triangle ABC.

3. Construct the Orthocenter of triangle HBC.

4. Construct the Orthocenter of triangle HAB.

5. Construct the Orthocenter of triangle HAC.

6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

7. Conjectures? Proofs?

First, construct a triangle ABC and its orthocenter H. The orthocenter can be created from the intersection of the altitudes of triangle ABC.

Notice that 3 additional triangles (called orthic triangles) were formed by constructing the orthocenter of triangle ABC. They are HAB, HAC and HBC. Now let's find their orthocenters one at a time.

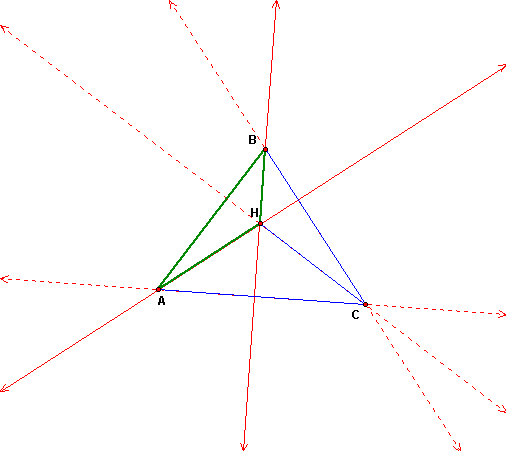
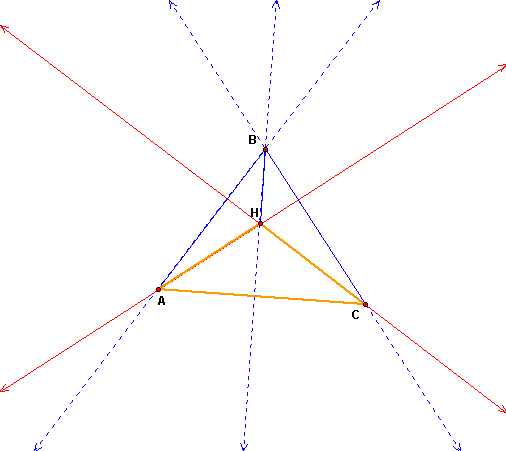
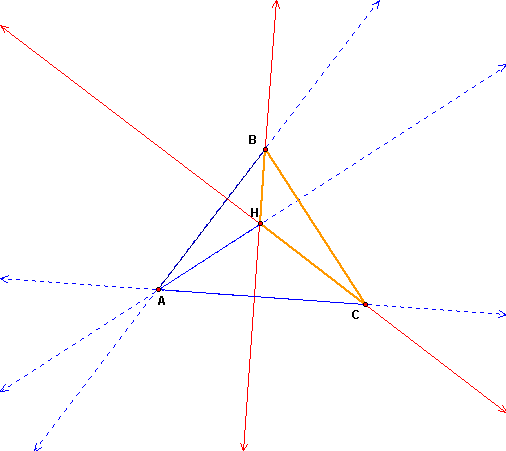
As you can see, the orthocenters of the three triangles are the vertices of the original triangle. Does this relationship hold true for triangle ABC whether it is acute, right, or obtuse? 

Click here to use the script tool and investigate.

Now construct the circumcircles for each of the four triangles...ABC, HAB, HAC, and HBC.

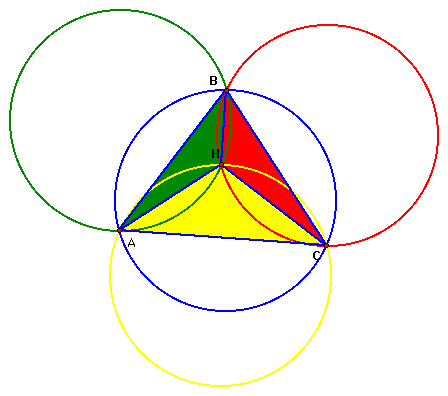
Notice that the size of all four circles looks the same. How do you know for sure? Try switching the vertices of triangle ABC with H(the orthocenter).

Click here to use the script tool and investigate on your own

 Conjectures:

If you move A to H, C to H and B to H, you can see that the circumcircles are all the same size. Therefore, when the orthocenter is one of the vertices of the original triangle it is apparent that the circumcircles of the triangles are congruent. This seems to hold true however, even if the orthocenter is not one of the vertices of the triangle. Therefore, the circumcircle of a triangle and its orthic triangles are always congruent.