
Lisa Brock & Scott Burrell
Assignment 9
Investigations With Pedal
Triangles
We begin this
investigation by constructing triangle ABC and its pedal triangle for arbitrary
point P. The pedal triangle is
formed by connecting the intersections of the perpendicular lines from P to the
each of the sides of the triangle.
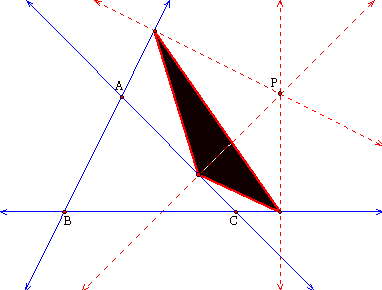
We will now look at what
happens when P is the centroid, G, of triangle ABC.
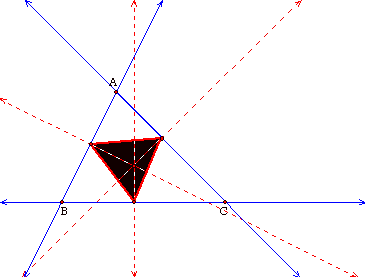
The pedal triangle is
completely inside triangle ABC and appears equilateral.
We will now look at what
happens when P is the incenter, I, of triangle ABC.
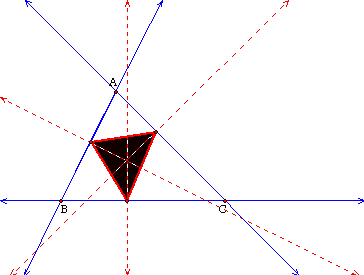
The pedal triangle remains
inside of triangle ABC but no longer appears to be equilateral.
We will now look at what
happens when P is the orthocenter, H, of triangle ABC.
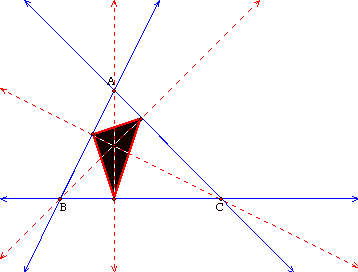
The pedal triangle is the
orthic triangle. This makes sense
because the orthocenter is the intersection of the altitudes of triangle
ABC. The three points used to form
the orthic triangle are feet of the altitudes. So the vertices of the orthic triangle are formed from the
perpendicular from H to each side.
Since P is located at H in this case, the vertices of the pedal
triangles are the same as the vertices of the orthic triangle.
Now we well look at
whether this holds if the orthocenter, H, is outside of triangle ABC.
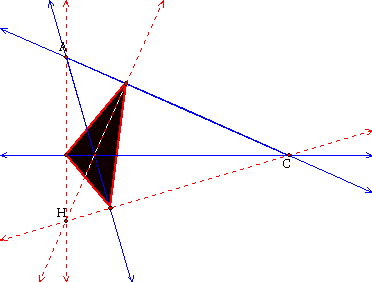
This relationship holds
when the orthocenter is outside of triangle ABC.
We will now look at what
happens when P is the circumcenter, C, of triangle ABC.
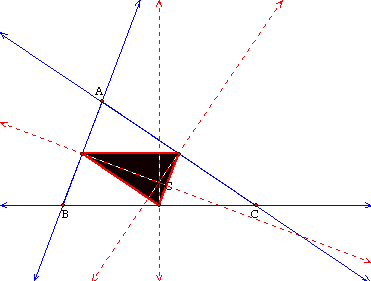
The pedal triangle is the
medial triangle. This makes sense
because the vertices of the medial triangle are the midpoints of the sides of
triangle ABC. The circumcenter is
perpendicular to each side through its midpoint. Therefore, when P is the circumcenter, the vertices of the
pedal triangle would be the midpoints of the sides of triangle ABC.
Now we will see if this
relationship holds when the circumcenter is outside of triangle ABC.
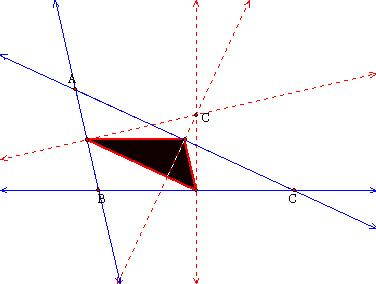
The relationship holds
when the circumcenter is outside of the triangle.
Now we will look at what
happens when P is on one of the sides of triangle ABC.
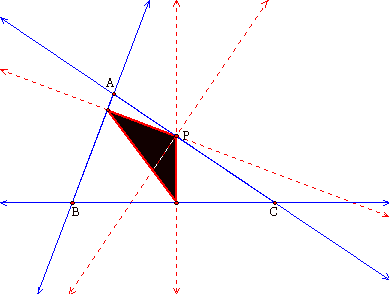
P becomes one of the
vertices of the pedal triangle.
Now we will look at what
happens when P is vertex, B, of triangle ABC.
When P is one of the
vertices of triangle ABC, the pedal triangle is degenerate (it collapses).