Objective: Use
the AAS Theorem to prove two triangles congruent. Use the HL Theorem
to prove two right triangles congruent.
So far we have learned three methods for proving
triangles congruent; the SSS, SAS and ASA Postulates. In this
lesson, we will add the AAS Theorem and the HL Theorem.
AAS Theorem
If two angles and a non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.
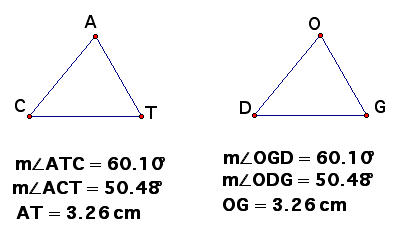
Given: Angle T congruent to Angle G; Angle C congruent to Angle D; DG congruent to AT
Prove: Triangle CAT congruent to triangle DOG
| Statements | Reasons |
| 1. Angle T congruent Angle G; Angle C congruent Angle D | 1. Given |
| 2. DG congruent AT | 2. Given |
| 3. Angle A congruent to Angle D | 3. If 2 angles in a triangle are congruent to 2 angles in another triangle, then third angles congruent. |
| 4. Triangle CAT congruent to triangle DOG | 4. ASA |
Example Proof using overlapping triangles:
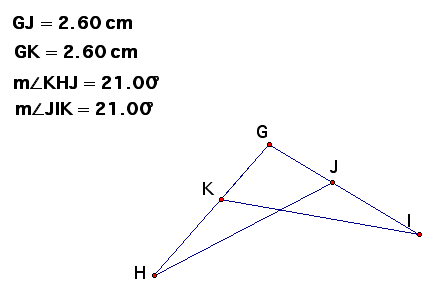
Given: GJ congruent to GK; Angle H congruent to Angle I
Prove: Triangle GHJ congruent to Triangle GIK
| 1. Angle H congruent to Angle I | 1. Given |
| 2, Angle G congruent to Angle G | 2. Reflexive Property |
| 3. GJ congruent to GK | 3. Given |
| 4. Triangle GHJ congruent to Triangle GIK | 4. AAS |
HL Theorem
If the hypotenuse and a leg of one right triangle are congruent to the corresponding parts of another right triangle, then the triangles are congruent.
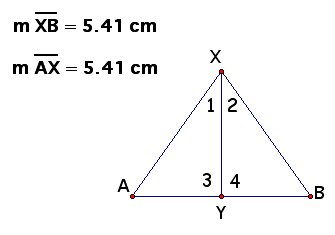
Given: XY perpendicular to AB; XA congruent to XB
Prove: Angle 1 congruent to Angle 2
| 1. XY perpendicular to AB; XA congruent to XB | 1. Given |
| 2. Angle 3 and Angle 4 are right angles | 2. Definition of perpendicular |
| 3. XY congruent XY | 3. Reflexive |
| 4. Triangle XYA congruent to Triangle XYB | 4. HL Theorem |
| 5. Angle 1 congruent Angle 2 | 5. CPCTC |
Summary of Ways to Prove Two Triangles Congruent
All triangles: SSS, SAS, ASA, AAS
Right triangles: HL
Exercise Proofs (Write in 2 column form)
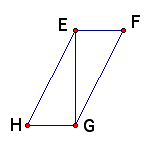
1. Given: EF perpendicular to EG; HG perpendicular to EG; EH congruent to GF
Prove: Angle H congruent to Angle F
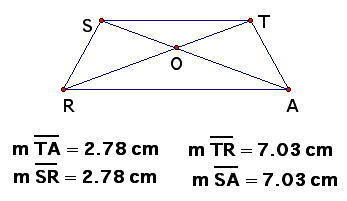
2. Given: RT congruent to AS; RS congruent to AT
Prove: Angle TSA congruent to Angle STR