Investigating the graph of
Write-up by
Blair T. Dietrich
EMAT 6680
What happens to the graph of 
as
a varies?
This investigation will explore the relationship between the quadratic coefficient a and the related graph.
(Note that a necessary condition is that 
;
otherwise, the equation would not be quadratic.)
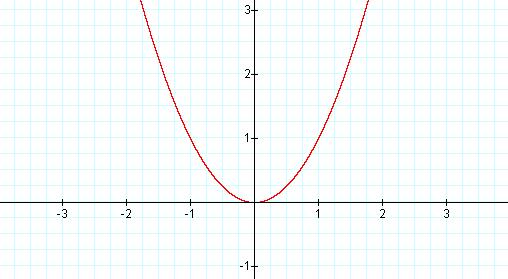
If we let a = 1, we have the equation 
. We will refer to
this as the "parent" equation.
What happens as a gets larger than 1?
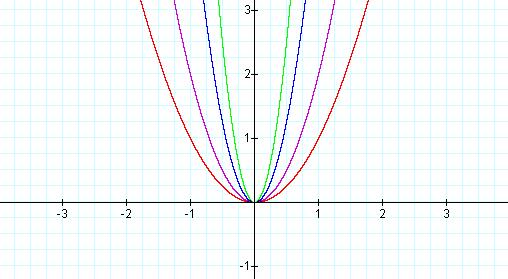
Notice that as a gets larger, the graph of the parabola gets narrower than the graph of the parent equation.
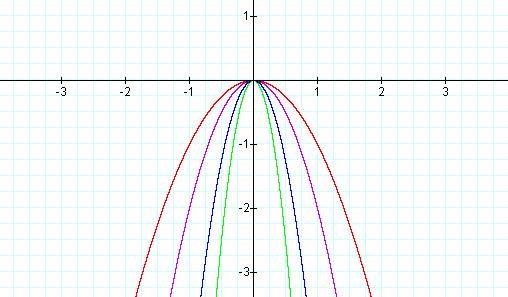
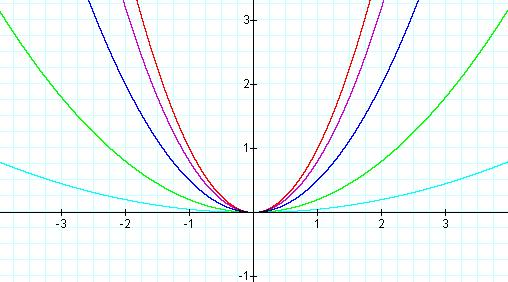
If we start by letting a = -1, we have the reflection of the parent graph about the x-axis.
As we allow this (negative) value of a to have greater magnitude (i.e. as |a| gets larger), the graph again becomes narrower.
Below are some examples for negative values of a.
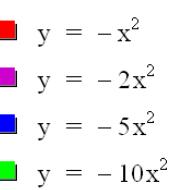
Now let us consider values of a in the open interval (0,1):
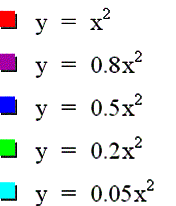
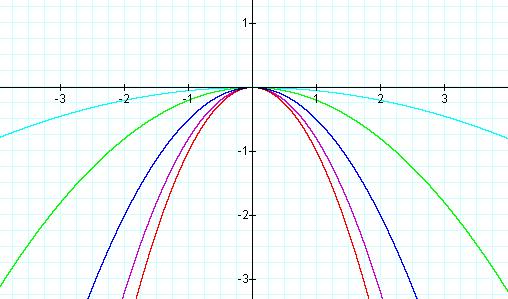
Notice that values of a that are closer to zero result in a wider graph than that of the parent graph.
Values of a in the interval (-1,0) yield a similar result, i.e. values closer to zero yield a wider graph. The only difference is that a negative value of a results in a graph that has been reflected about the x-axis.
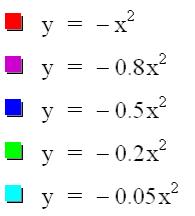
To try your own values of a, click here.