Proving the concurrency of
the three perpendicular bisectors
of the sides of a triangle.
Write-up by
Blair T. Dietrich
EMAT 6680
Assignment #4 Problem #12
Given triangle ABC, prove that the three perpendicular bisectors of the sides of the triangle are concurrent.
Proof:
Construct the perpendicular bisectors of ![]() and
and ![]() , namely
, namely ![]() and
and ![]() , intersecting at point I.
, intersecting at point I.
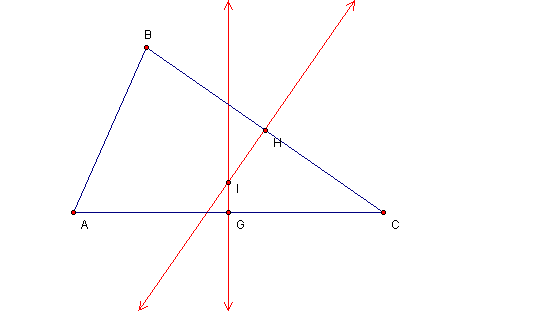
The point of concurrency I can be shown to be equidistant from points A and C:
Angle AGI and angle CGI are right
angles since ![]() .
.
![]() and
and![]() are right triangles by the definition of a right triangle.
are right triangles by the definition of a right triangle.
![]() since G is the
midpoint of
since G is the
midpoint of ![]() .
.
![]() by the reflexive
property.
by the reflexive
property.
![]() by the Leg-Leg Theorem for right triangles.
by the Leg-Leg Theorem for right triangles.
![]() since corresponding parts of congruent triangles are
congruent.
since corresponding parts of congruent triangles are
congruent.
Therefore, AI = CI by the definition of congruent segments
Similarly, it can be shown that ![]() and that I is equidistant from points B and C.
and that I is equidistant from points B and C.
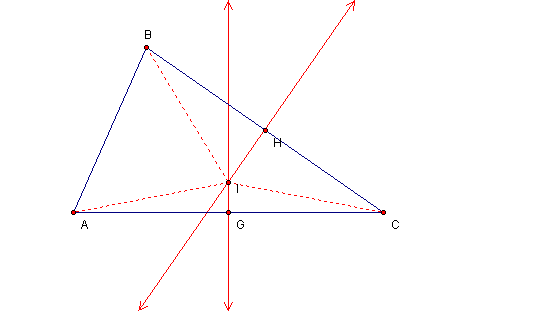
It follows then that, since ![]() and
and ![]() ,
, ![]() by the Transitive Property.
by the Transitive Property.
We now must show that the point I lies on the perpendicular
bisector of ![]() :
:
Construct a
line through I that is perpendicular to ![]() . Label the point of
intersection J.
. Label the point of
intersection J.
Angle AJI and angle BJI are right angles by the definition of perpendicular lines.
![]() and
and![]() are right triangles by the definition of right triangles.
are right triangles by the definition of right triangles.
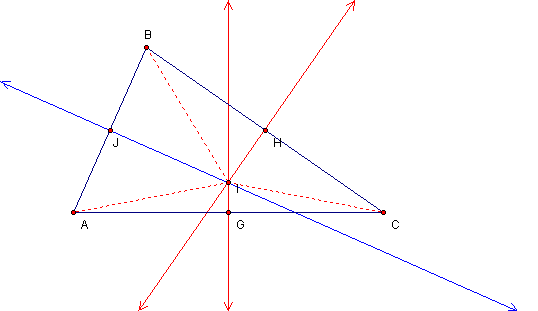
It has been shown that the three perpendicular bisectors are concurrent at point I.
Note that this point I is not necessarily on the interior of triangle ABC, nor does it necessarily lie on the angle bisectors of triangle ABC; therefore, this point I is not, in general, the incenter of the triangle.
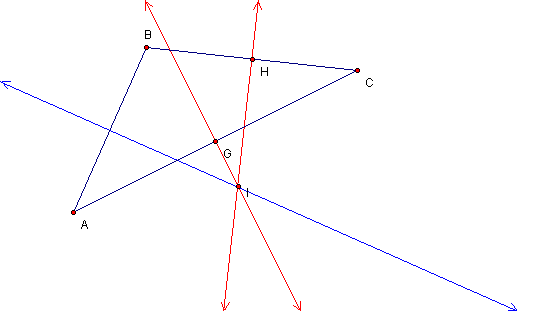
Another example showing that I is not the incenter.
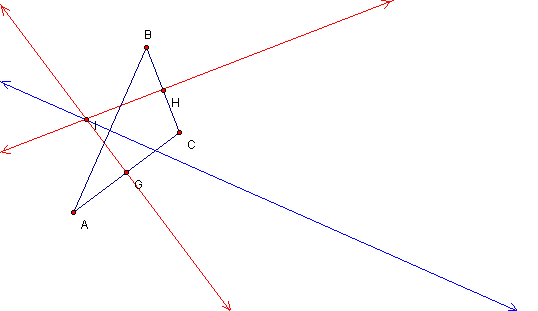
However, in each case the perpendicular bisectors are concurrent.