Investigating relationships
between a triangle and
the triangle constructed by using its medians.
Write-up by
Blair T. Dietrich
EMAT 6680
Assignment #6 Problem #2
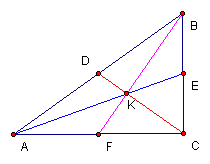
This investigation will focus on some relationships between a triangle ABC and the triangle constructed by using its medians.
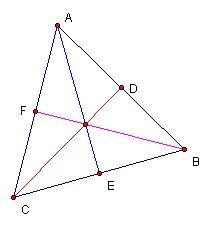
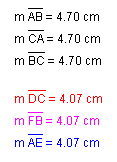
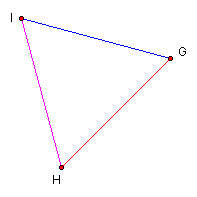
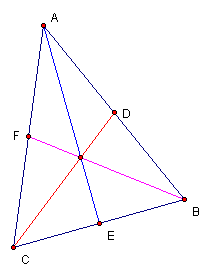
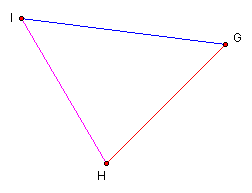
Consider the equilateral triangle ABC shown below. Each of AE, BF, and CD are medians of triangle ABC. A second triangle (GIH) was constructed having sides with lengths equal to the lengths of the three medians of triangle ABC. Note that triangle GIH is also equilateral.
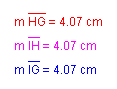
Now consider isosceles triangle ABC. Similarly, triangle GIH was constructed using sides of the same length as the medians AE, BF, and CD. Note that triangle is GIH is also isosceles.

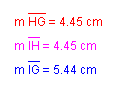
Try
your own triangles using the GSP file here.
What happens if we let triangle ABC be a right triangle? Here angle ACB is a right angle. Note that triangle GIH is not, in general, a right triangle.
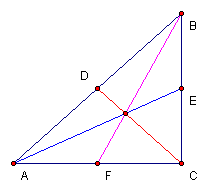

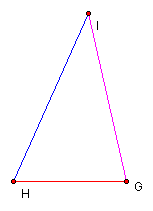

When any two of the medians of right triangle ABC form a right angle, the triangle GIH will be a right triangle.

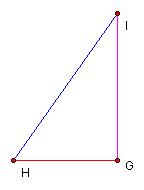

Try
your own right triangles using the GSP file here.