Tangent Circles
Write-up by
Blair T. Dietrich
EMAT 6680
Assignment #7
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
The construction:
Given circles O and B and a point A on circle O. Construct the line containing O and A.
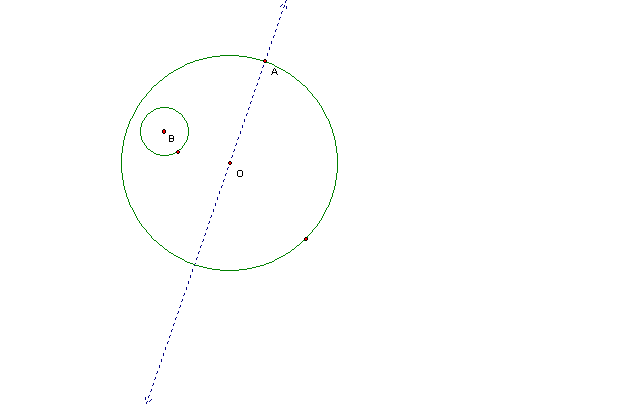
Construct a circle centered at A that has the same radius as circle B. Circle A intersects line OA in two places. Label the outside point of intersection C and constuct the segment from B to C.
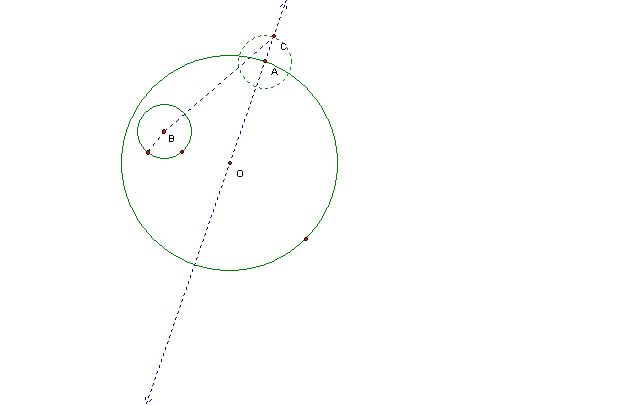
Construct the perpendicular bisector of BC. This line intersects OA at point D.

The distance from D to A is the same as the distance from D to the edge of circle B. By constructing a circle centered at point D that passes through A, we have a circle that is tangent to both circle O and circle B.

Investigations:
MORE CIRCLES
When point A travels around the edge of circle O, the midpoint of segment BC used in the construction traces out a circle (shown in blue). This is true regardless of the position of circles O and B.

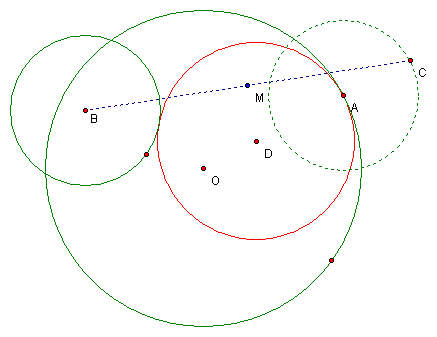
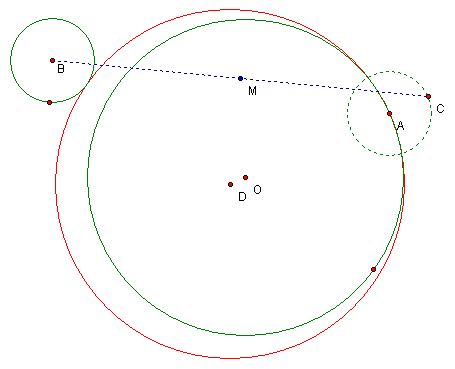
To investigate this on your own, click here.
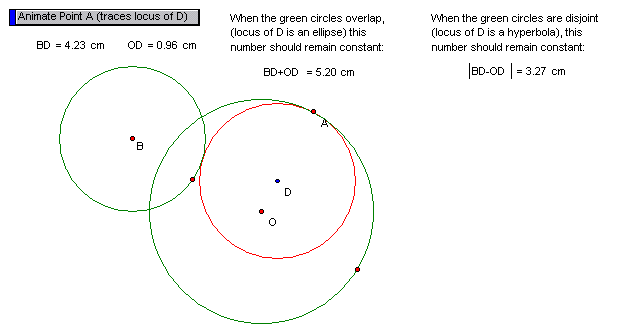
ELLIPSES and HYPERBOLAS
When point A travels around the edge of circle O, the center point of circle D traces out an ellipse (shown in blue). This will always be true as long as circle B lies entirely or partially inside circle O.

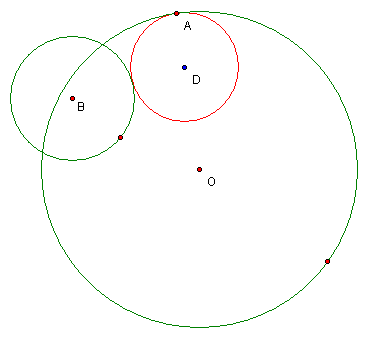
However, if circle B is completely outside of circle O, the locus of points traced by point D is a hyperbola.

By definition, the sum of the distances from a point on an ellipse (point D) to each of the two foci (points O and B) has to remain constant. Also, the magnitude of the difference between the distances from a point on a hyperbola (D) to each of the focal points (O and B) must remain constant. Notice these relationships hold true as you investigate here.
(A sample screen shot is shown below.)