Pedal Triangles
Write-up by
Blair T. Dietrich
EMAT 6680
Assignment #9
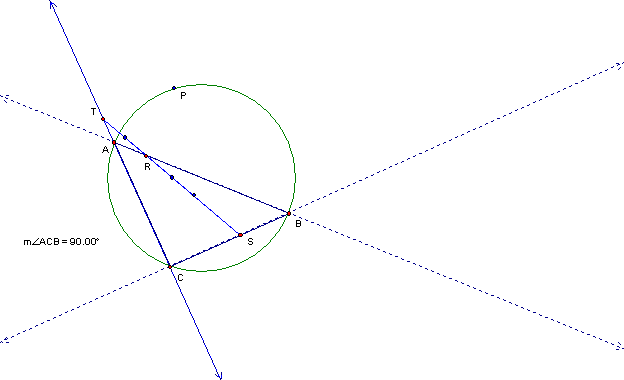
This investigation will focus on pedal triangles. Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

If P is the centroid of triangle ABC, the pedal triangle appears to be the medial triangle but, in fact, it is not.
Shown below are two graphs. The first one shows P coinciding with the centroid G. In this picture, it can be seen that the points R, S, and T are not the midpoints of segments AB, BC, and CA, respectively.
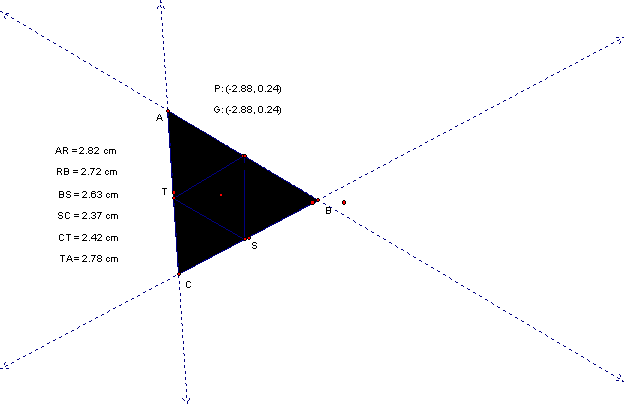
The second one shows the points R, S, and T coinciding with the midpoints of segments AB, BC, and CA, respectively, and that P is clearly not the same as G.

Notice that sometimes the Pedal Triangle is in the interior of triangle ABC and sometimes it is not. Look at this animation and try to decide how the position of P affects the location of the Pedal Triangle. You can also stop the animation and drag the point P yourself.
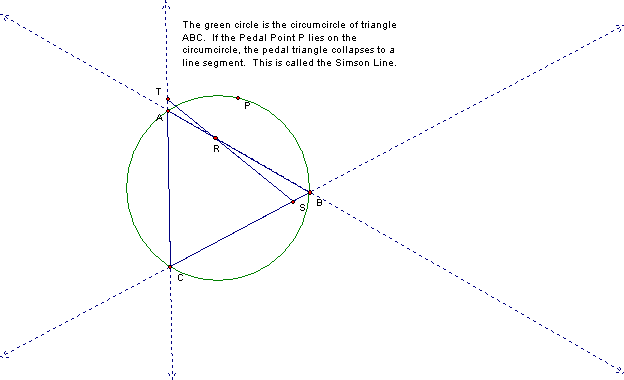
When the Pedal Point is moved along the circumcircle, the locus of the Simson Line forms a triangular-shaped region "under stress" called a deltoid.
Try this one yourself. Click here.
What happens if the midpoints of the sides of the Pedal Triangle are traced? In the graph below, the pedal point P was allowed to circumnavigate the circumcircle. Notice that the midpoints trace out three ellipses.
Notice that when triangle ABC is a right triangle, one of the midpoints traces out the path of a circle rather than an ellipse.
To observe an animation of the traced midpoints of the sides of the Pedal Triangle, click here.