Using parametric equations
to generate linear equations.
Write-up by
Blair T. Dietrich
EMAT 6680
Assignment #10 Problems #5 & 7
This investigation will focus on the use of parametric equations to generate linear equations.
What type of graph does the pair of parametric equations 
and 
yield? To investigate this question the equations
were graphed for a range of values for k for each selected pair of
values for a and b. Some
examples follow:
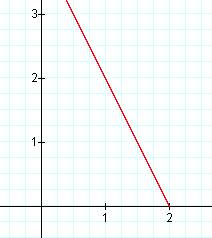
k = -2 k = -1 k = 0
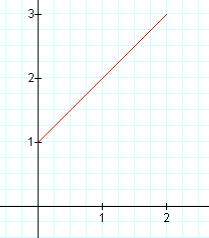
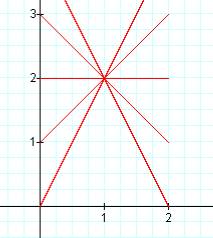
k = 1 k = 2 k=-2,-1,0,1,2 all superimposed
In this case, a segment of a line is "captured" between the vertical lines x = 0 and x = 2. As k is changed, the slope of the line segment changes. In fact, the slope of the line segment equals the value of k. Also, each of these line segments has a common point of (1,2). This point seems to be a "pivot" point for the segment as k (the slope) is varied.
Try animating "k" on the GCF file here.
Similarly…
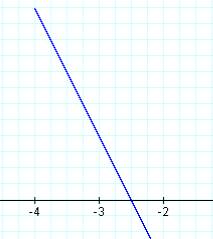
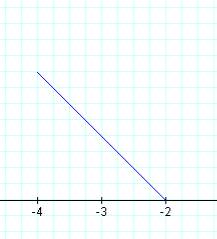
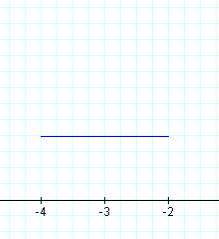
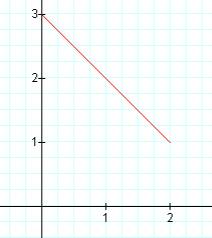
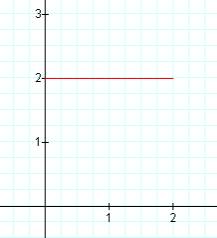
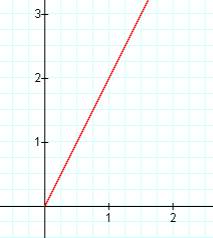
k = -2 k = -1 k = 0
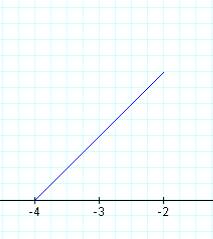
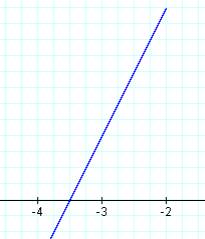
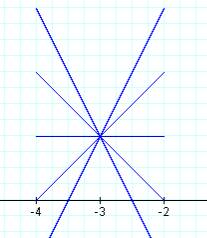
k = 1 k = 2 k=-2,-1,0,1,2 all superimposed
In this case, a segment of a line is "captured" between the vertical lines x = -4 and x = -2. As k is changed, the slope of the line segment changes. In fact, the slope of the line segment equals the value of k. Also, each of these line segments has a common point of (-3,1). This point seems to be a "pivot" point for the segment as k (the slope) is varied.
Try animating "k" on the GCF file here.
It appears that a and b yield the coordinates
of the pivot point. This point is the
point translated from (0,0) in the equation 
where k is the
slope of the line. This can be shown by
solving the equation 
for t and
substituting into the other equation:
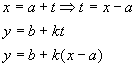
This equation is clearly the equation 
that has been translated
horizontally a units and vertically b units.
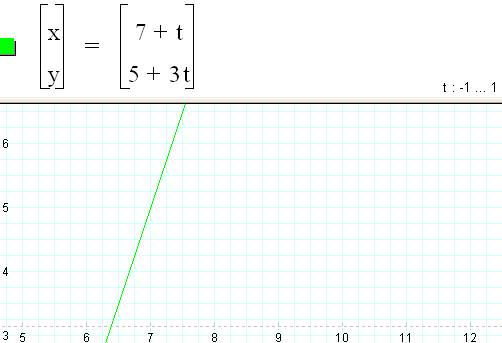
With this in mind, it seems clear that in order to graph the line segment through (7,5) with a slope of 3, the parametric equations needed would be the following:
